
Sia
下午 11:37 5月5日周日
翻译可用
完成
邦助 I Haozhe Liu I 关阘
mäbius
Engineering Mechanics -Statics 1004 1004UAC ( 2024 S1 Combined)
SUM 8 - Centroids
SUM 8 - Centroids
剩余时间:
- 试题 1
5 分数
THIS ASSIGNMENT CONTRIBUTES TO YOUR COURSE MARK.
Calculate the and coordinates of the centroid of the body shown in the diagram below, given and m.
Centroid coordinates:
提交试卷
退出并保存
远回
试题菜单
下一题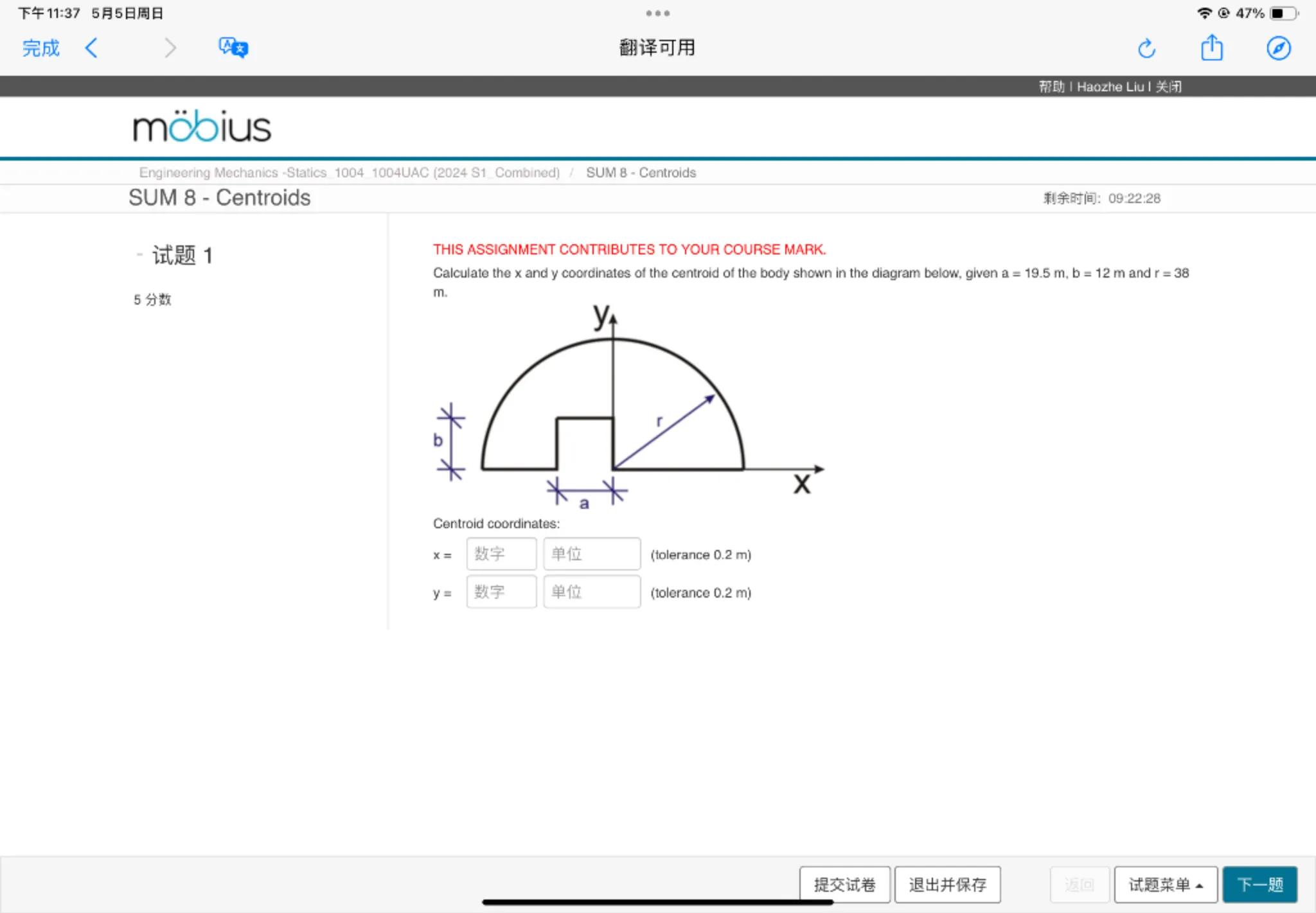

Answer from Sia
Posted 10 months ago
Solution
a
Calculate the area of the quarter-circle and the rectangle
The area of the quarter-circle is $$ A_{circle} = \frac{1}{4} \pi r^2 $$ and the area of the rectangle is $$ A_{rectangle} = a \times b $$.
b
Calculate the centroid of the quarter-circle and the rectangle
The centroid of the quarter-circle is at $$ (\frac{4r}{3\pi}, \frac{4r}{3\pi}) $$ and the centroid of the rectangle is at $$ (\frac{a}{2}, \frac{b}{2}) $$.
c
Calculate the coordinates of the centroid of the composite shape
Use the principle of moments for the x-coordinate: $$ x_{centroid} = \frac{A_{circle} \times \frac{4r}{3\pi} - A_{rectangle} \times \frac{a}{2}}{A_{circle} - A_{rectangle}} $$ and for the y-coordinate: $$ y_{centroid} = \frac{A_{circle} \times \frac{4r}{3\pi} - A_{rectangle} \times \frac{b}{2}}{A_{circle} - A_{rectangle}} $$.
d
Substitute the given values into the equations
For the x-coordinate: $$ x_{centroid} = \frac{\frac{1}{4} \pi (38)^2 \times \frac{4 \times 38}{3\pi} - 19.5 \times 12 \times \frac{19.5}{2}}{\frac{1}{4} \pi (38)^2 - 19.5 \times 12} $$ and for the y-coordinate: $$ y_{centroid} = \frac{\frac{1}{4} \pi (38)^2 \times \frac{4 \times 38}{3\pi} - 19.5 \times 12 \times \frac{12}{2}}{\frac{1}{4} \pi (38)^2 - 19.5 \times 12} $$.
e
Calculate the numerical values for the centroid coordinates
After performing the calculations, we find the x and y coordinates of the centroid.
Answer
The x and y coordinates of the centroid are calculated to be (with the given tolerances of 0.2 m):
Key Concept
The centroid of a composite shape can be found by taking the weighted average of the centroids of the individual shapes, weighted by their respective areas.
Explanation
The centroid coordinates are calculated by dividing the moment of the area about the axes by the total area of the shape. The moments are found by multiplying the area of each part by the coordinates of its centroid.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question