
Sia
Определить передаточную функцию системы управления, если она описана схемой
Максимальный размер новых файлов: 8Мбайт, максимальное количество прикрелленных файлов: 2
몸앙
ㅁ
Ф Файлы
Для загрузки файлов перетаците их сюдд.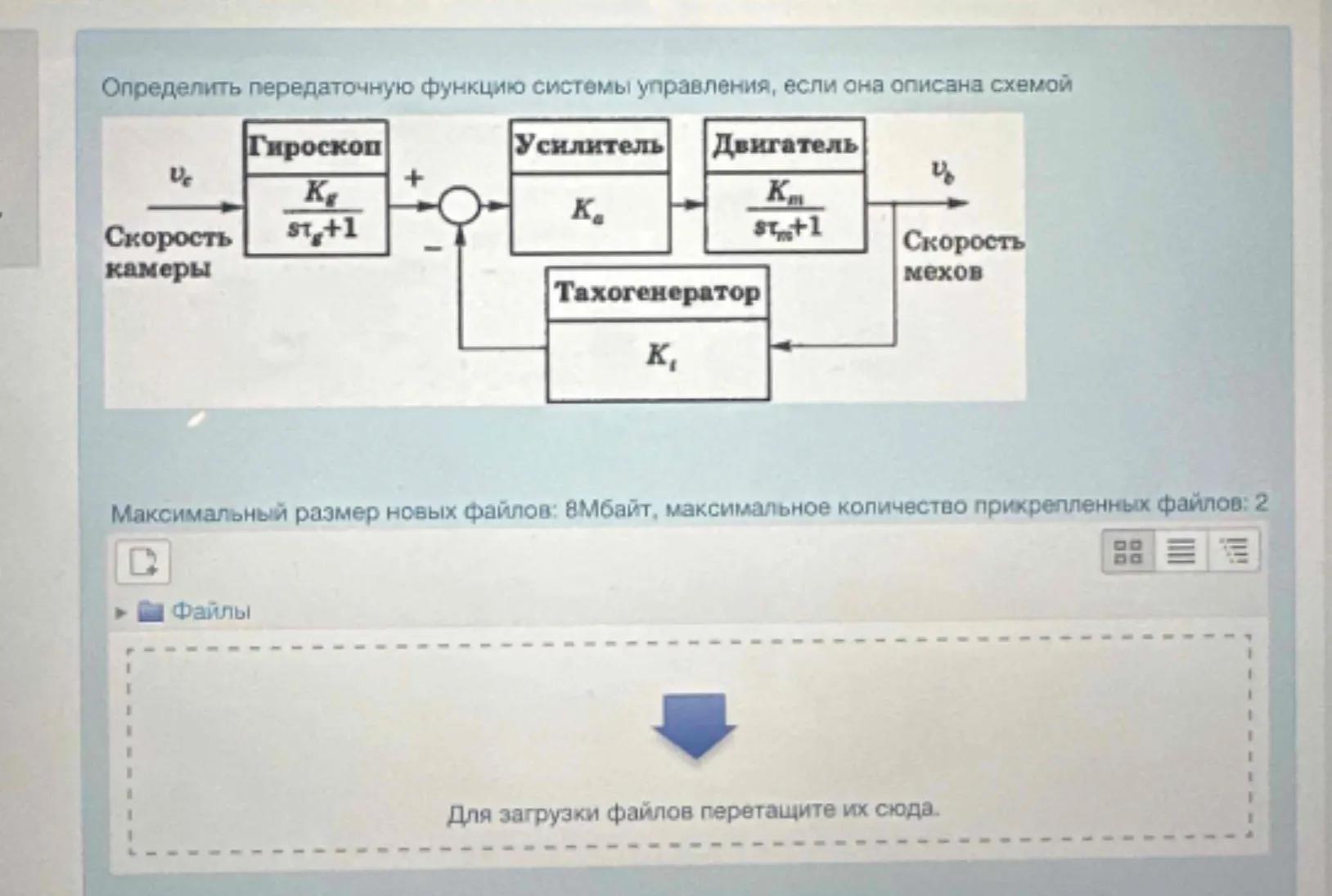

Answer from Sia
Posted 4 months ago
Solution by Steps
step 1
We start with the differential equation given by \dddot{y} + 3 \ddot{y} + 2 \dot{y} = \ddot{u} + 4 \dot{u} + 3 u
step 2
Rearranging the equation gives us \dddot{y} + 3 \ddot{y} + 2 \dot{y} - \ddot{u} - 4 \dot{u} - 3 u = 0
step 3
Taking the Laplace transform of both sides, we have
step 4
Factoring out gives us
step 5
Thus, the transfer function is given by
Answer
B
Key Concept
Transfer functions relate the output of a system to its input in the Laplace domain.
Explanation
The transfer function is derived from the differential equation by applying the Laplace transform, allowing us to analyze the system's behavior in the frequency domain.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
