Asksia AI LOGO

Sia

linadpb's Question
Math
Posted 5 months ago

kwyk.fr
Devenir voya...
Une disserta....
I'apologie de...
et récurrenc...
Navigo : Sou.
Impossible □\square
Entraine-toi
Devoirs
Bilan
obsolète ce qui peut provoquer des incompatibilités (boutons non fonctionnels, problèmes d'affichage,...) fin de vous garantir une expérience optimale, nous vous conseillons de le mettre à jour.

Dérivation - compléments
Attention, les réponses aux QCM de rattrapage ne rapportent que 20\% des points.
Quelle est la dérivée de la fonction ff ? On admettra qu'elle est dérivable sur chaque intervalle contenu dans son domaine de définition D=RD=\mathbb{R}.
5−2sin⁡(−8x−9)−7
\frac{5}{-2 \sin (-8 x-9)-7}

Valider ✓\checkmark
Suivant I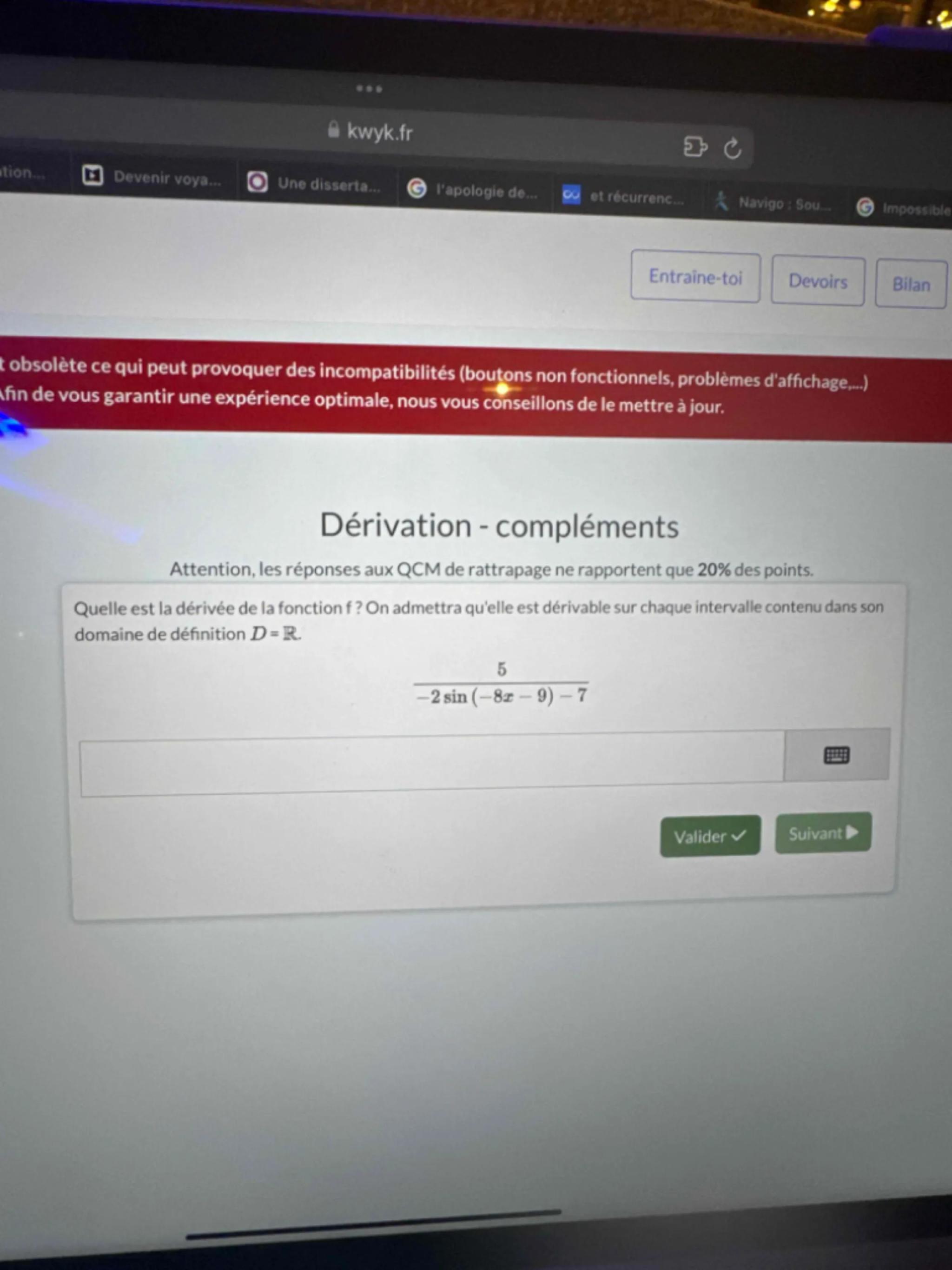
Sign in to unlock the answer
Answer from Sia
Posted 5 months ago
Solution by Steps
step 1
We start with the function defined as f(x)=−2sin⁡(−8x−9)−7 f(x) = -2 \sin(-8x - 9) - 7 . To find the derivative, we apply the chain rule
step 2
The derivative is calculated as f′(x)=−2⋅(−8)cos⁡(−8x−9)=16cos⁡(−8x−9) f'(x) = -2 \cdot (-8) \cos(-8x - 9) = 16 \cos(-8x - 9)
step 3
We can express the cosine function in terms of exponential functions: 16cos⁡(−8x−9)=8e−8ix−9i+8e8ix+9i 16 \cos(-8x - 9) = 8 e^{-8ix - 9i} + 8 e^{8ix + 9i}
step 4
The function is defined for all real numbers, so the domain is D=R D = \mathbb{R} . The range of f′ f' is {y∈R:−16≤y≤16} \{ y \in \mathbb{R} : -16 \leq y \leq 16 \}
Answer
The derivative of the function is f′(x)=16cos⁡(−8x−9) f'(x) = 16 \cos(-8x - 9)
Key Concept
Derivatives represent the rate of change of a function.
Explanation
The derivative calculated shows how the function f(x) f(x) changes with respect to x x , and the range indicates the possible values of the derivative.

Not the question you are looking for? Ask here!

Enter question by text

Enter question by image

Unlock Smarter Learning with AskSia Super!

Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.

30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question