
Sia
Incorrect.
The series converges by the alternating series test. How many terms give a partial sum, , within 0.02 of the sum, , of the series?
i 50
eTextbook and Media
Hint
Assistance Used
Since the series converges and is an alternating series of the form , by Theorem 9.9: Error Bounds for Alternating Series you know .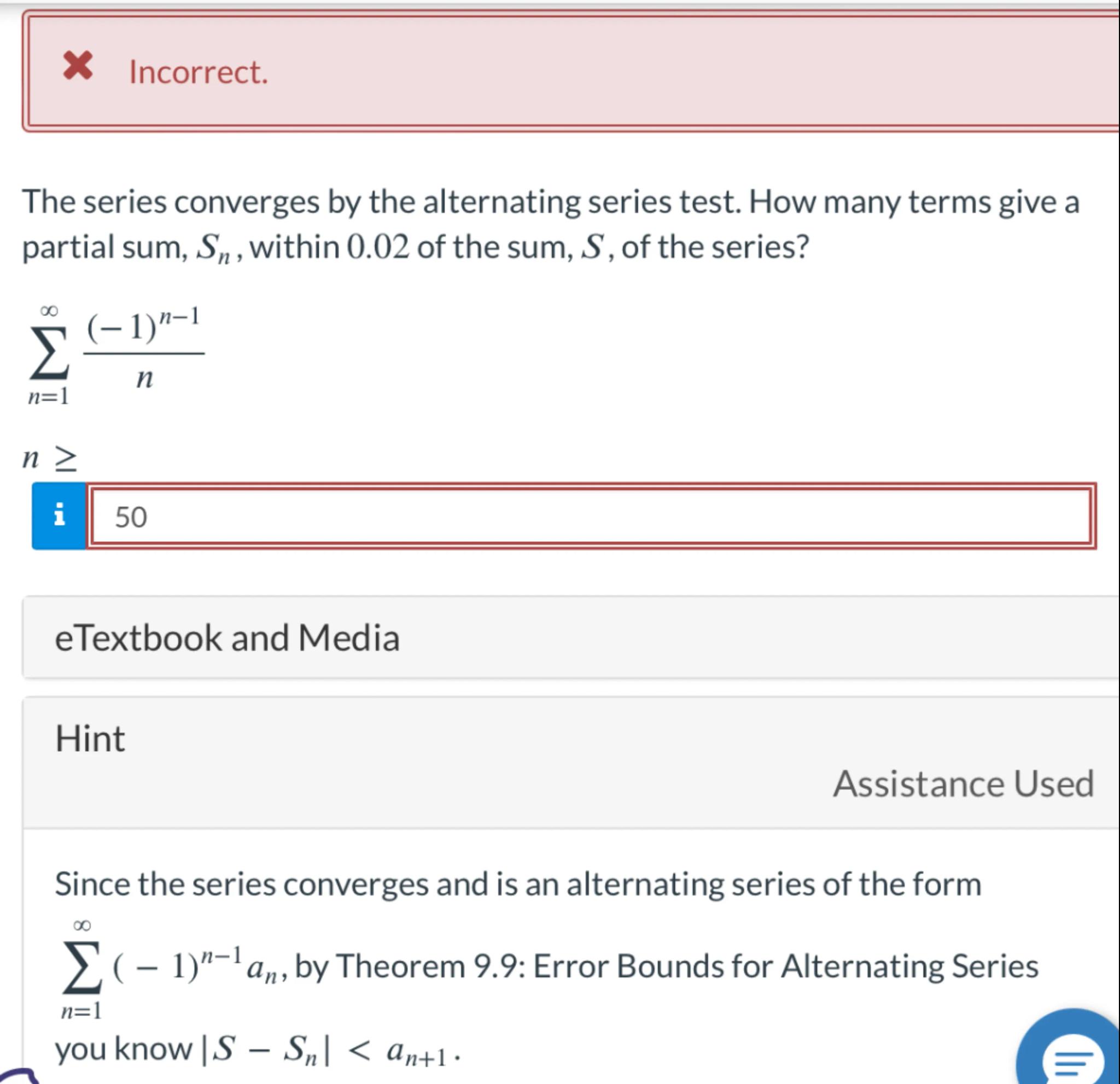

Answer from Sia
Posted 7 months ago
Solution by Steps
step 1
To determine the number of terms needed to get a partial sum within 0.02 of the total sum of the series, we use the error bound for alternating series. According to Theorem 9.9, for an alternating series of the form , the error is less than
step 2
The given series is . Here,
step 3
To find the number of terms such that the error is within 0.02, we need
step 4
Since , we set up the inequality
step 5
Solving for , we get , which simplifies to
step 6
Therefore, we need at least 50 terms to ensure the partial sum is within 0.02 of the total sum
Answer
50
Key Concept
Error Bound for Alternating Series
Explanation
The error bound for an alternating series states that the absolute error is less than the next term in the series. By ensuring the next term is less than the desired error margin, we can determine the number of terms needed.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question