
Sia

Question
Math
Posted 9 months ago
Which graph could be a solution to the logistic differential equation
Choose 1 answer: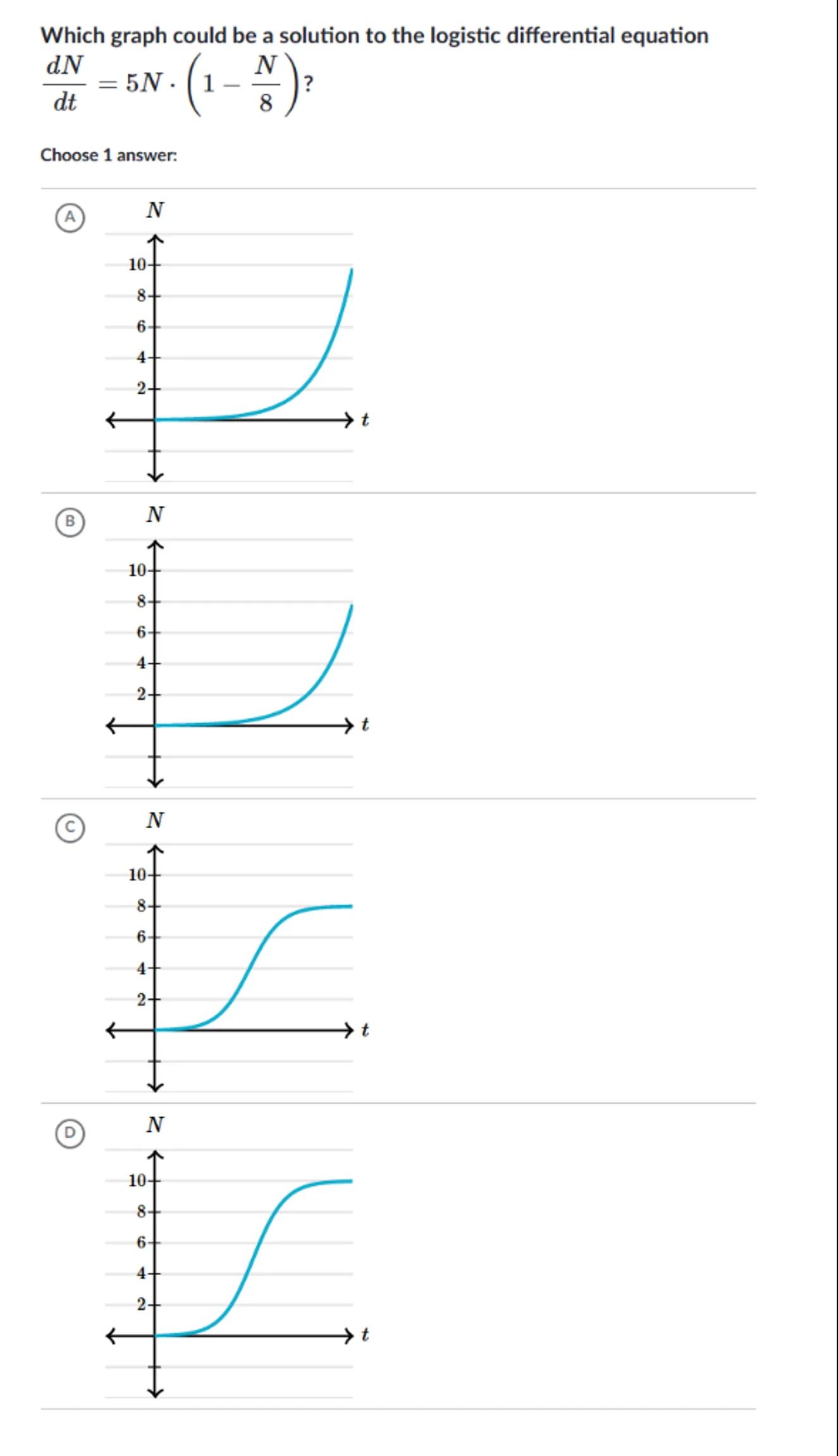

Answer from Sia
Posted 9 months ago
Solution by Steps
step 2
This is a first-order nonlinear ordinary differential equation
step 3
To solve it, we use the method of separation of variables. Rewrite the equation as:
step 4
Integrate both sides:
step 5
The left side can be integrated using partial fractions:
step 6
This gives:
step 7
Simplify and solve for :
step 8
Exponentiate both sides:
step 9
Let , then:
step 10
Solve for :
step 11
The general solution is: where
step 12
Given the initial condition , solve for :
step 13
This gives , so the specific solution is:
step 14
The solution approaches 8 as
step 15
Therefore, the graph that shows starting at 1 and leveling off near 8 is the correct one
A
Key Concept
Logistic Growth
Explanation
The logistic differential equation models population growth that starts exponentially but levels off as it approaches a carrying capacity.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question