
Sia
What is the for the following reaction from the equilibrium constant at the temperature given?
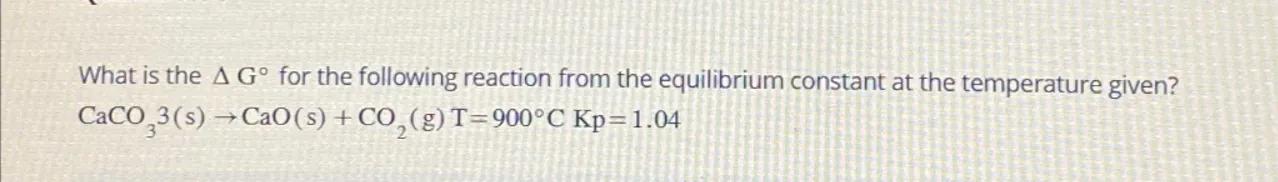

Answer from Sia
Posted 9 months ago
Solution
1
Identify the reaction: The given reaction is at with
2
Use the relationship between $\Delta G^{\circ}$ and $K_p$: The standard Gibbs free energy change () for a reaction can be calculated using the equation:
where is the gas constant () and is the temperature in Kelvin
3
Convert temperature to Kelvin:
4
Calculate $\Delta G^{\circ}$:
Answer
Key Concept
Relationship between Gibbs free energy change and equilibrium constant
Explanation
The standard Gibbs free energy change () for a reaction can be determined from the equilibrium constant () using the equation . This relationship shows how the spontaneity of a reaction is related to its equilibrium position.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question