
Sia

Question
Math
Posted 10 months ago
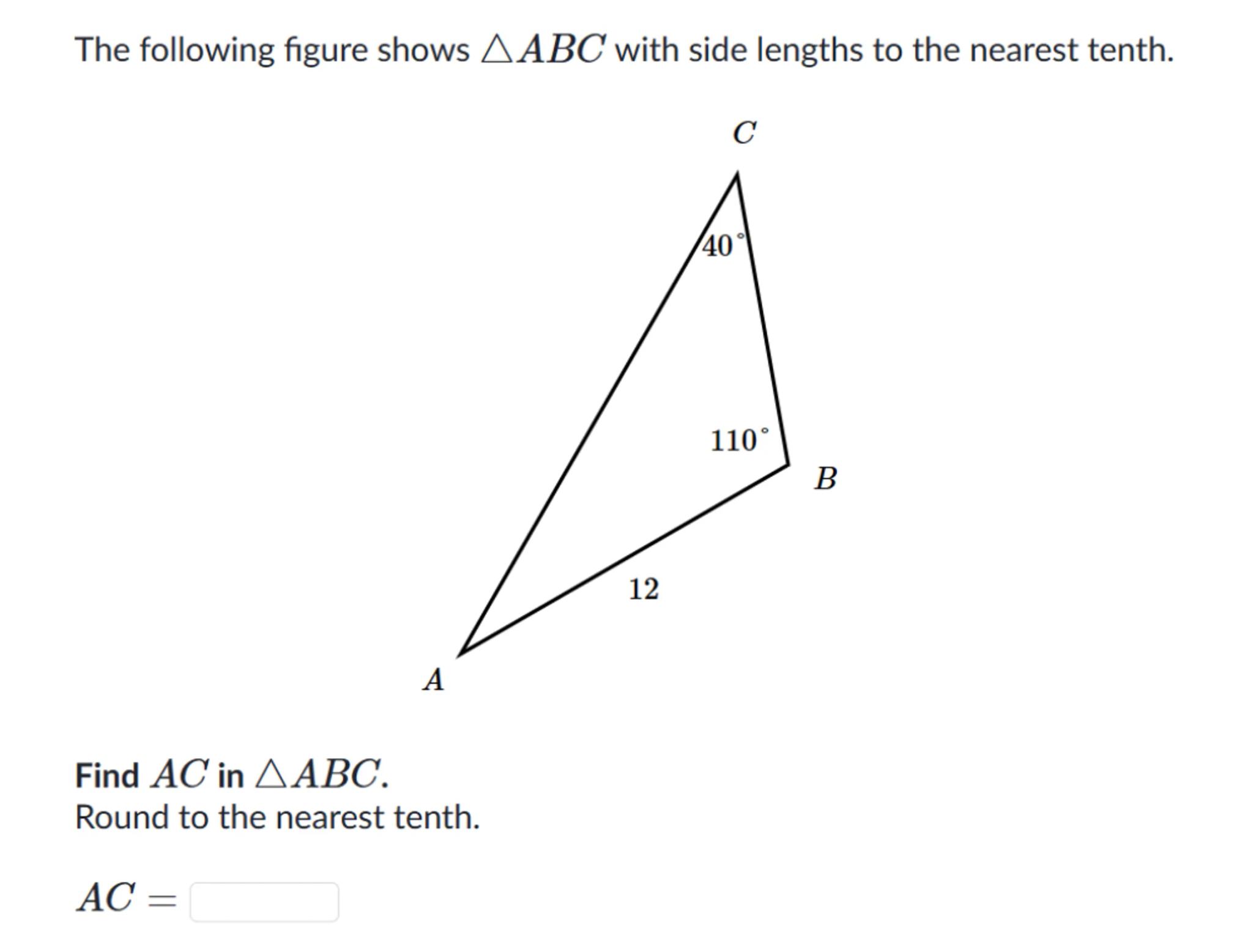
The following figure shows with side lengths to the nearest tenth.
Find in .
Round to the nearest tenth.

Answer from Sia
Posted 10 months ago
Solution by Steps
step 1
To find the length of side AC, we can use the Law of Sines, which relates the lengths of sides of a triangle to the sines of its opposite angles
step 2
The Law of Sines states that , where , , and are the lengths of the sides opposite to angles , , and respectively
step 3
Given that units, , and , we can find by using the fact that the sum of angles in a triangle is
step 4
Calculating :
step 5
Now we can apply the Law of Sines to find :
step 6
Substituting the known values into the Law of Sines:
step 7
Solving for :
step 8
Since , the equation simplifies to:
step 9
Calculate using a calculator and round to the nearest tenth:
Answer
[Insert final answer here after calculation]
Key Concept
Law of Sines
Explanation
The Law of Sines is used to find unknown side lengths in a triangle when given two angles and one side.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question