
Sia

Question
Math
Posted 9 months ago
The base of a solid is the region bounded by the parabola and the line .
Cross-sections perpendicular to the -axis are isosceles right triangles with the hypotenuse lying in the base.
Determine the exact volume of solid .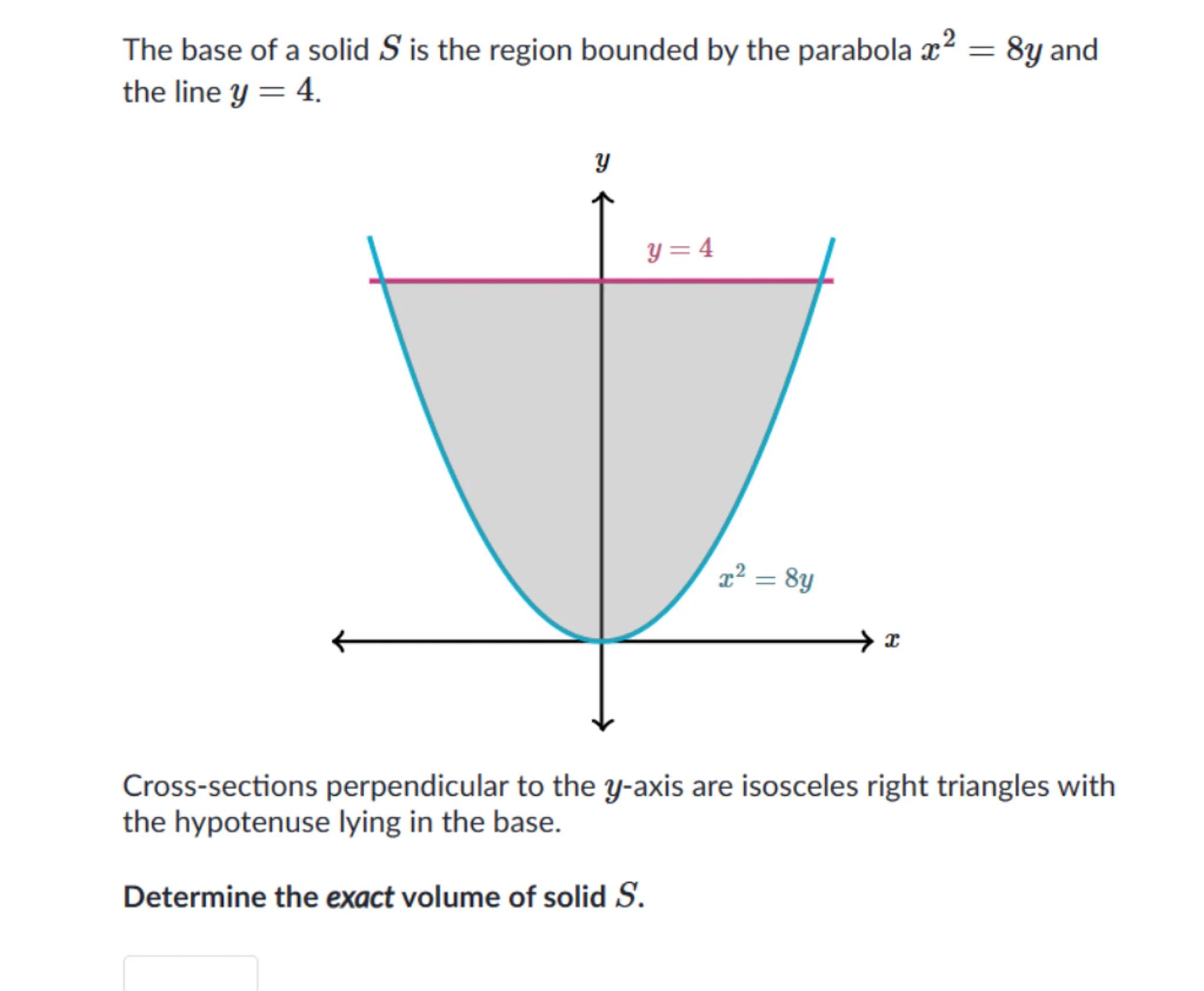

Answer from Sia
Posted 9 months ago
Solution by Steps
step 1
The base of the solid is the region bounded by the parabola and the line . We need to find the volume of the solid with cross-sections perpendicular to the -axis that are isosceles right triangles with the hypotenuse lying in the base
step 2
The length of the hypotenuse of each isosceles right triangle is the distance between the points where the parabola intersects the line . Solving , we get , so . Thus, the length of the hypotenuse is
step 3
For an isosceles right triangle, the relationship between the hypotenuse and the legs is . Therefore,
step 4
The area of each cross-sectional triangle is
step 5
To find the volume of the solid, we integrate the area of the cross-sections along the -axis from to :
step 6
Evaluating the integral, we get
Answer
The exact volume of the solid is cubic units.
Key Concept
Volume of a solid with known cross-sectional area
Explanation
To find the volume of a solid with a known cross-sectional area, integrate the area of the cross-sections along the axis perpendicular to the cross-sections.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question