
Sia
Part 1
First pattern has been designed for you. You are required to find the functions and the circle used for this design, based on the description below.
The following functions/relations have been used to design this pattern:
- one logarithmic function and its inverse
- two cubic functions
- one circle
Recommended function types:
Mathematical rules used for this design:
(i) the four functions start at the origin.
(ii) logarithmic function and its exponential inverse end at
(iii) logarithmic function has
(iv) the point of inflection of the top cubic (green function) is located at
(v) the maximum value of the top cubic (green function) aligns vertically with the stationary point of inflection of the bottom cubic (blue function)
(vi) the minimum point of the top cubic (green function) is located at
(vii) the area of the circle is one third of the area between the two cubic functions and its centre aligns with the minimum point of the top cubic.
(viii) the two cubic functions always meet on the logarithmic function.
Based on the above information find:
1. The four functions and the equation of the circle.
2. Calculate the areas between each curve combination (use of technology indicated).
Refer to the cubic functions found from above rules. Assume that their respective found and values do not change.
Yeor 12 Mothernatical Methods
2021
By varying only their leading coefficients, and respectively, investigate:
3. The change in the area between the two cubic functions with respect to the total area (area between the logarithm and the exponential function).
4. How and vary as the area between the two cubic functions approaches a maximum or a minimum.
Hence,
5. Find two cubic functions such that the area between them is of the total area(area between the logarithm and the exponential function).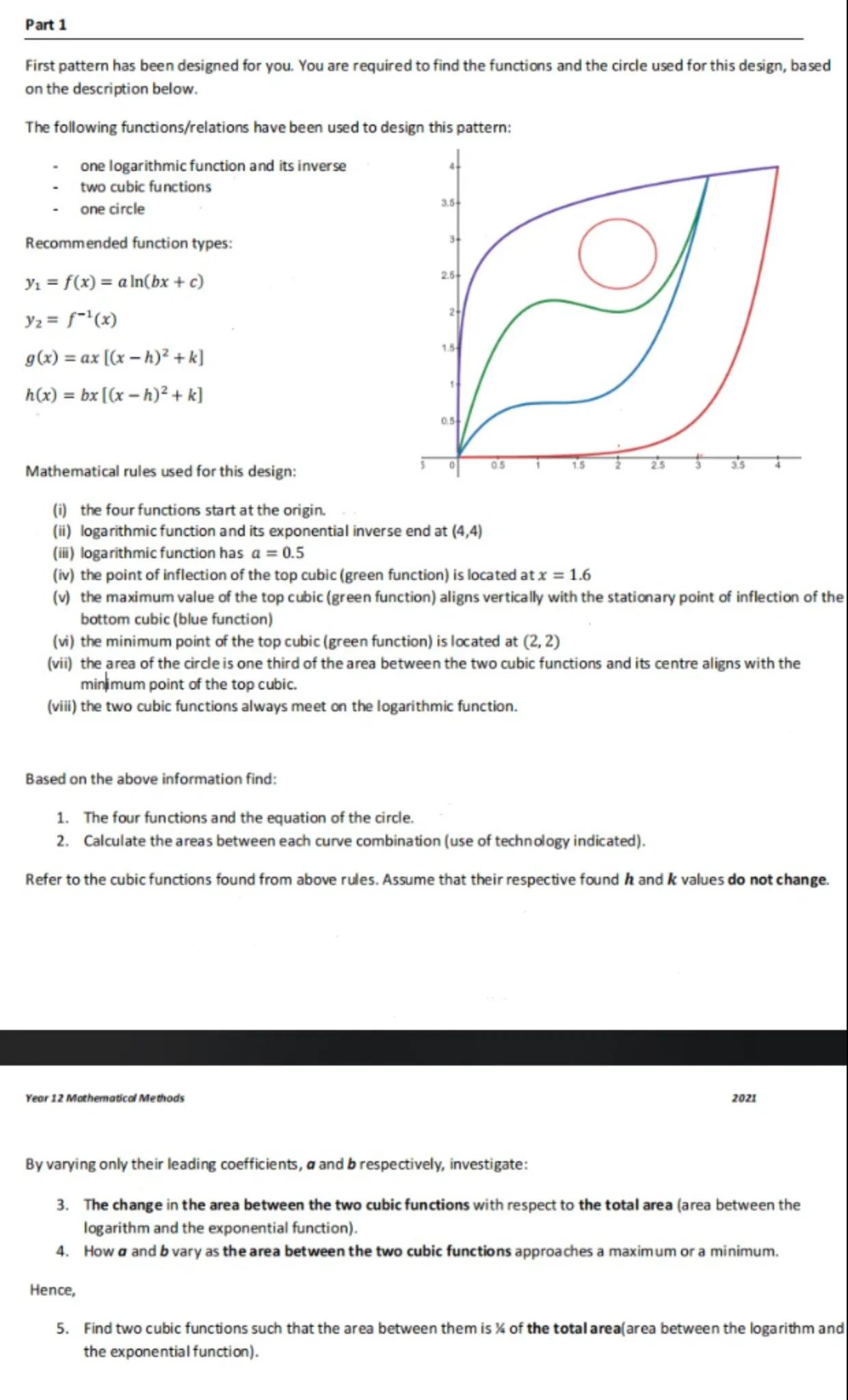

Answer from Sia
Posted 9 months ago
Solution by Steps
step 1
Given the logarithmic function and its inverse , we know from the problem that
step 2
To find and , we solve the equation for and . From the Asksia-LL calculator, we have
step 3
Next, we solve for and . From the Asksia-LL calculator, we have
step 4
For the cubic functions and , we use the given conditions to find , , , and
step 5
Given that the point of inflection of the top cubic (green function) is at , and the minimum point is at , we solve for , , and
step 6
The area of the circle is one third of the area between the two cubic functions, and its center aligns with the minimum point of the top cubic. We use this information to find the radius of the circle
step 7
To find the total area between the logarithmic function and its inverse, we integrate the difference between the two functions from to
step 8
To find the area between the two cubic functions, we integrate the difference between and from to
step 9
To investigate how and vary as the area between the two cubic functions approaches a maximum or minimum, we analyze the leading coefficients of the cubic functions
step 10
Finally, to find two cubic functions such that the area between them is of the total area, we adjust the leading coefficients and accordingly
Answer
The four functions and the equation of the circle are found using the given conditions and solving for the unknowns. The areas between each curve combination are calculated using integration.
Key Concept
Integration and solving for unknowns in functions
Explanation
The problem involves finding specific functions and calculating areas between them using integration, based on given conditions.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question