
Sia

Question
Math
Posted 9 months ago
Let be the region in the first quadrant that is inside the polar curve and inside the polar curve , as shown in the graph. The curves intersect at .
What is the area of ?
Use a graphing calculator and round your answer to three decimal places.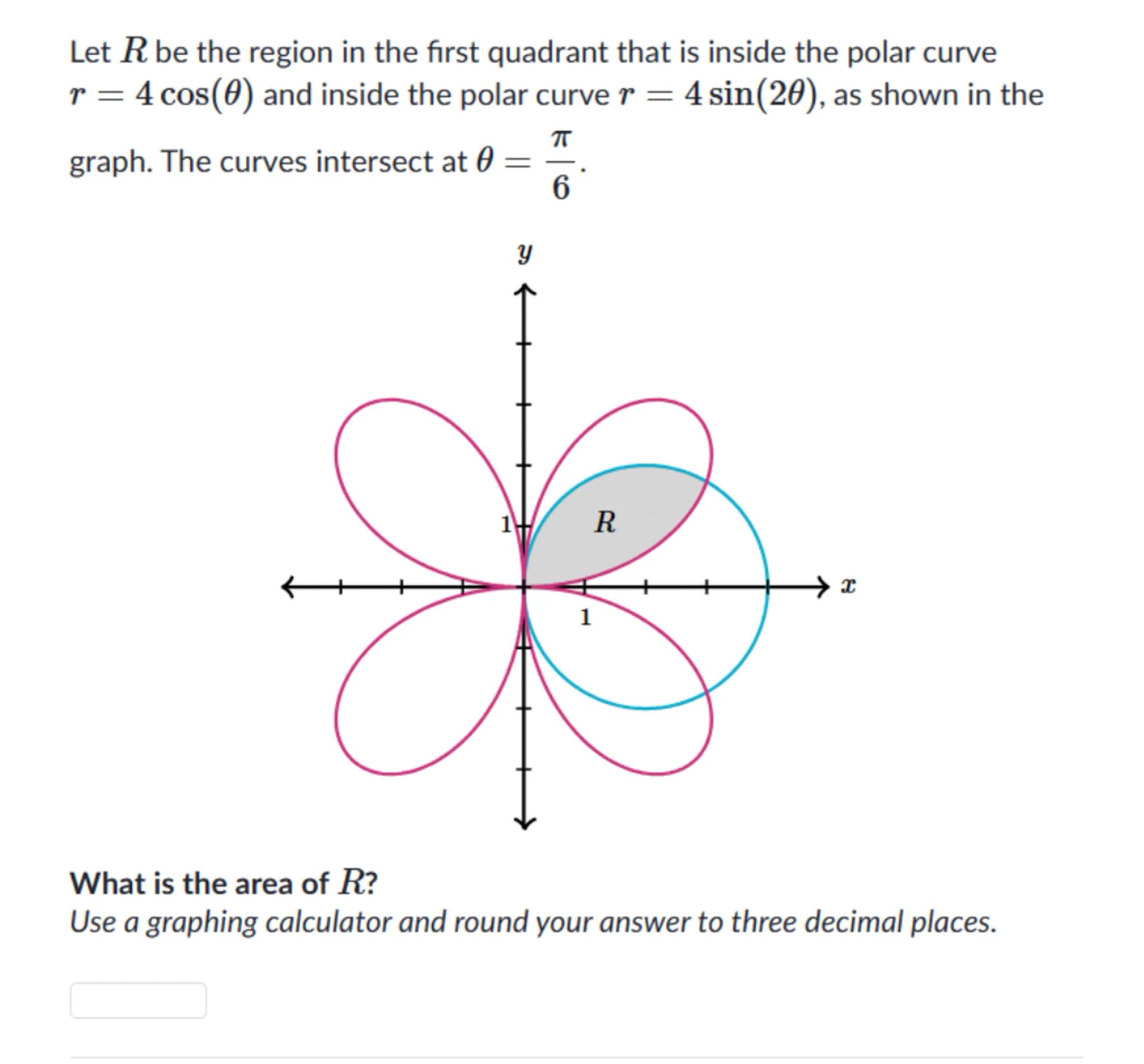

Answer from Sia
Posted 9 months ago
Solution by Steps
step 1
To find the area of the region inside the polar curves and , we need to set up the integrals for each curve and then subtract the second integral from the first
step 2
First, we calculate the integral of from to :
step 3
Next, we calculate the integral of from to :
step 4
Finally, we subtract the result of the second integral from the first integral to find the area of :
Answer
The area of the region is approximately square units.
Key Concept
Area of a region bounded by polar curves
Explanation
To find the area of a region bounded by two polar curves, we integrate the square of the radius function for each curve over the given interval and then subtract the smaller area from the larger area.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question