
Sia

Question
Math
Posted 9 months ago
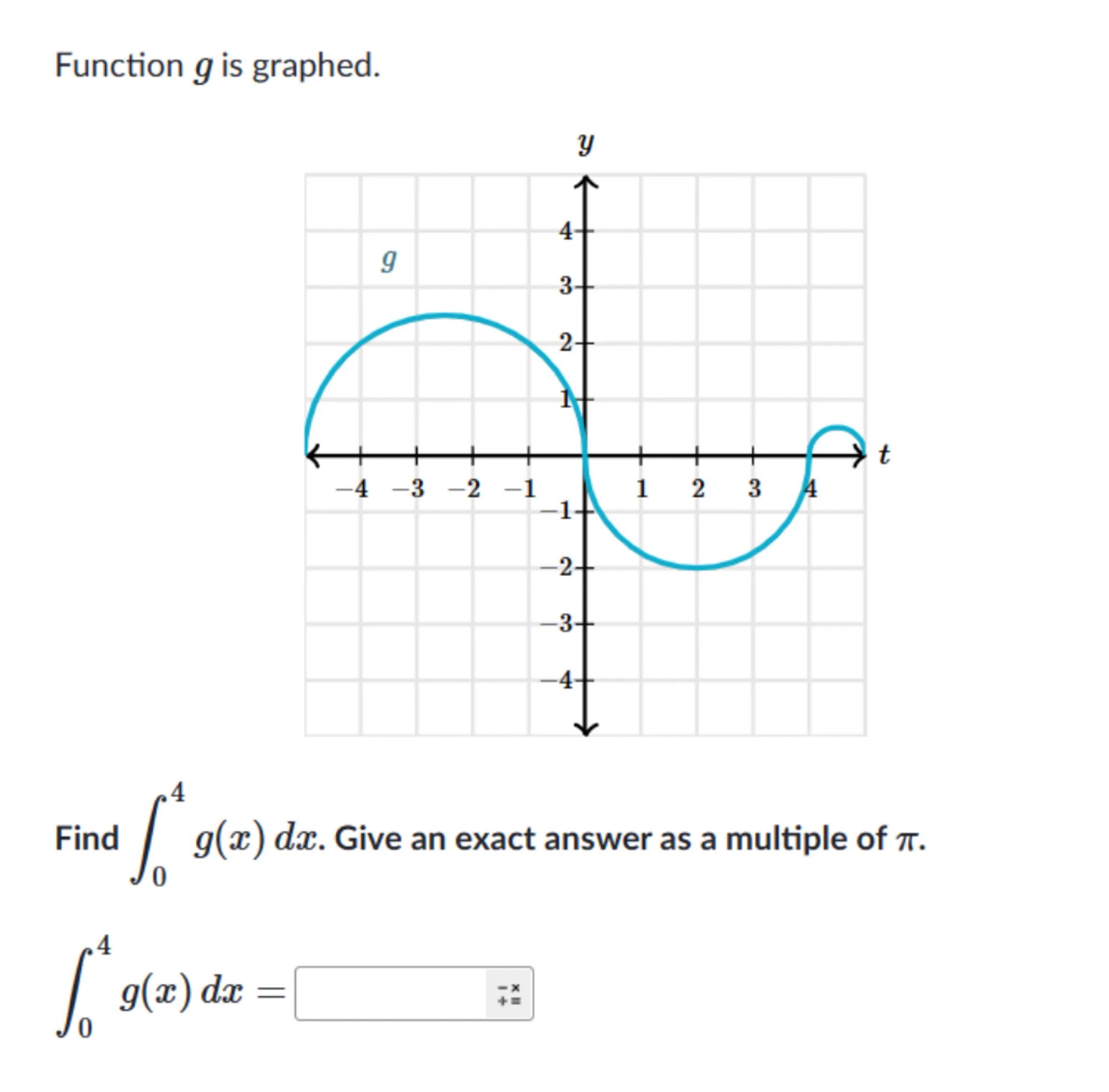
Function is graphed.
Find . Give an exact answer as a multiple of .

Answer from Sia
Posted 9 months ago
Solution by Steps
step 1
To find the integral , we need to analyze the graph of the function from to
step 2
From the graph, we observe that decreases from to and then increases from to
step 3
The area under the curve from to is a triangle with base and height . The area of this triangle is . Since the function is below the x-axis, this area is negative:
step 4
The area under the curve from to is another triangle with base and height . The area of this triangle is . Since the function is above the x-axis, this area is positive:
step 5
Adding these areas together, we get the total area under the curve from to :
Answer
Key Concept
Area under the curve
Explanation
The integral of a function over an interval can be found by calculating the areas of the regions under the curve, taking into account whether the function is above or below the x-axis.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question