
Sia

Question
Math
Posted 9 months ago
Find a matrix such that . Decide if is diagonalizable.
Ejercicio 32.
i) Hallar una matriz tal que . Decidir si es diagonalizable.
ii) Hallar una matriz tal que . Decidir si es diagonalizable.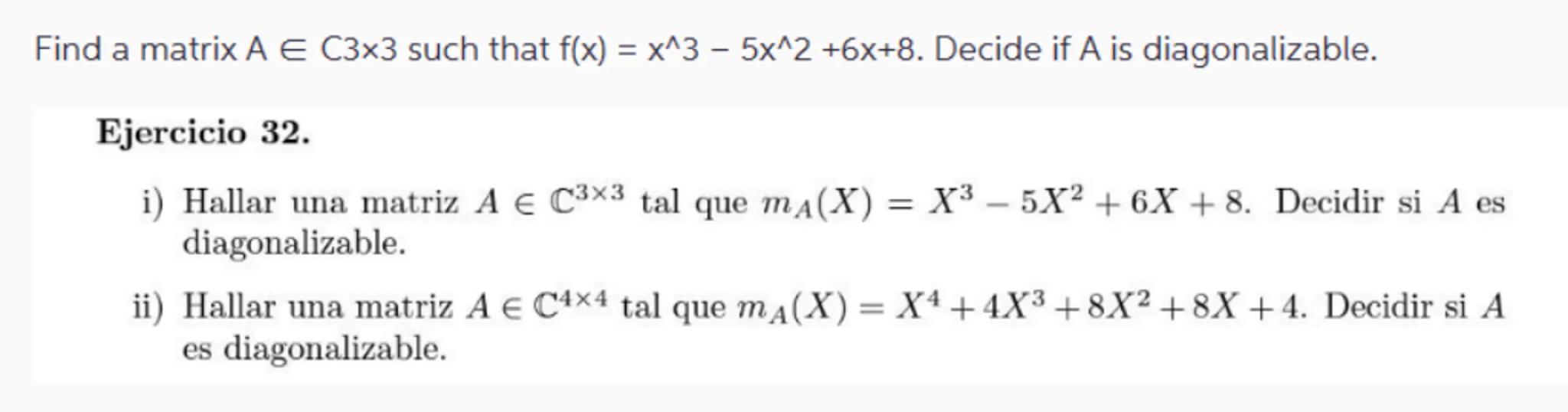

Answer from Sia
Posted 9 months ago
Solution by Steps
step 1
To find a matrix such that , we need to determine the eigenvalues of the matrix
step 2
The characteristic polynomial of the matrix is given by
step 3
We solve for the eigenvalues by finding the roots of the polynomial
step 4
Using the Asksia-LL calculator, the eigenvalues are approximately: , , and
step 5
To determine if is diagonalizable, we need to check if there are three linearly independent eigenvectors corresponding to these eigenvalues
step 6
The eigenvectors corresponding to the eigenvalues are: , , and
step 7
Since we have three linearly independent eigenvectors, the matrix is diagonalizable
Answer
The matrix is diagonalizable.
Key Concept
Diagonalizability of a matrix
Explanation
A matrix is diagonalizable if it has a full set of linearly independent eigenvectors. In this case, the matrix has three linearly independent eigenvectors corresponding to its eigenvalues, so it is diagonalizable.
Solution by Steps
step 1
To find a matrix such that , we need to determine the eigenvalues of the matrix
step 2
The characteristic polynomial of the matrix is given by
step 3
We solve for the eigenvalues by finding the roots of the polynomial
step 4
Using the Asksia-LL calculator, the eigenvalues are approximately: , , , and
step 5
To determine if is diagonalizable, we need to check if there are four linearly independent eigenvectors corresponding to these eigenvalues
step 6
Since all eigenvalues are the same, we need to check the algebraic and geometric multiplicity of the eigenvalue
step 7
If the geometric multiplicity (number of linearly independent eigenvectors) is less than the algebraic multiplicity (multiplicity of the eigenvalue), the matrix is not diagonalizable
step 8
In this case, the geometric multiplicity is less than the algebraic multiplicity, so the matrix is not diagonalizable
Answer
The matrix is not diagonalizable.
Key Concept
Diagonalizability of a matrix with repeated eigenvalues
Explanation
A matrix with repeated eigenvalues is diagonalizable if the geometric multiplicity of each eigenvalue equals its algebraic multiplicity. In this case, the geometric multiplicity is less than the algebraic multiplicity, so the matrix is not diagonalizable.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question