
Sia

Question
Math
Posted 8 months ago
Figure 1 shows a sketch of part of the curve with equation . The finite region , shown shaded in Figure 3, is bounded by the curve, the - axis and the lines and .
2. Figure 1 shows a sketch of part of the curve with equation . The finite region , shown shaded in Figure 3, is bounded by the curve, the -axis and the lines and .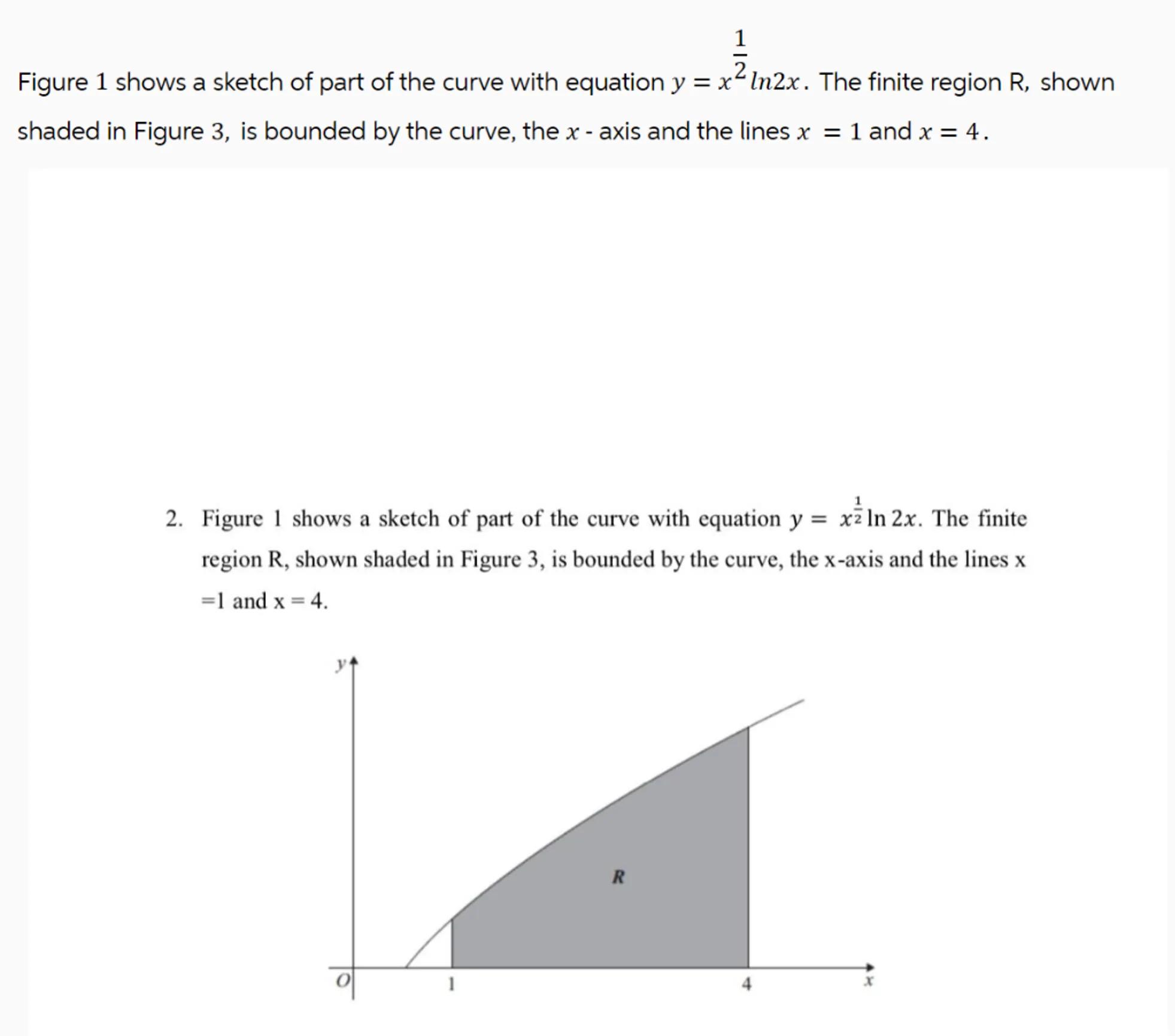

Answer from Sia
Posted 8 months ago
Solution by Steps
step 1
We need to evaluate the integral of the function from to
step 2
The integral is given by:
Using the result from the Asksia-LL calculator, we have:
step 3
The indefinite integral of the function is:
where is the constant of integration
step 4
Evaluating the definite integral from to :
Substituting the limits, we get:
Answer
The value of the integral is approximately 68.529.
Key Concept
Definite Integral
Explanation
The definite integral of a function over a specified interval gives the area under the curve of the function between the given limits. In this case, we evaluated the integral of from to .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question