Sia

alice15609's Question

Math

Posted 9 months ago

Exercise 3
Plane Geometry (II)
Level 1
Question 1
$A B C D$ is a parallelogram with $A B\|D C, A D\| B C$ as shown. The diagonal $B D$ is drawn.
(a) Prove that $\triangle A B D \equiv \triangle C D B$.
(b) Hence, explain why $A D=C B$ and $A B=C D$.
(c) What property of parallelograms have we proved?

Question 2
Prove that the opposite angles of a parallelogram are equal.
Year 9 (A1) Mathematics
Question 2*
$A B C D$ is a quadrilateral with $P, Q, R$ and $S$ being the midpoints of sides $A B, B C$, $C D$ and $D A$ respectively. Prove that $\triangle P B Q$ is similar to $\triangle A B C$, and hence that $P Q \| A C$. Thus prove quadrilateral $P Q R S$ is a parallelogram.
Exercise 2
Level 3

Question-1
$P Q R S$ is a trapezium with $P Q \| S R$. If $A, B$ and $C$ are the mid-points of $S P, P R$ and $Q R$ respectively, prove that:
(a) $A B \| S R$ :
(b) $B C \| P Q$;
(c) the points $A, B$ and $C$ are collinear.

Question 2*
In the figure, $A B C D$ is a trapezium, and $M N$ is parallel to $A B$ and $D C$. If $M N$ bisects the area $A B C D$, the length of $M N$, in centimetres, is
(A) $\sqrt{\frac{a^{2}+b^{2}}{2}}$
(B) $\frac{a^{2}+b^{2}}{a+b}$
(C) $\sqrt{a b}$
(D) $\frac{2 a b}{a+b}$
(E) $\frac{a+b}{2}$
(AMC)
Question 1*
Let $A B C D$ be a quadrilateral, with diagonals meeting at right angles at $M$.
(a) Find expressions for $A B^{2}, B C^{2}, C D^{2}$ and $A D^{2}$ in terms of $a, b, c$ and $d$.
(b) Hence show that $A B^{2}+C D^{2}=B C^{2}+A D^{2}$.

Question 2*
$A B C D$ is a quadrilateral with $\angle D A B=\angle D C B=90^{\circ}$. The bisectors of $\angle A D C$ and $\angle A B C$ meet the diagonal $A C$ at $E$ and $F$ respectively. Prove that $D E$ and $B F$ are parallel.
(b) Prove that $P R T S$ is a parallelogram.
Plane Geometry
Question 4
The diagram shows the parallelogram $A B C D$ with diagonal $A C$. The points $P$ and $Q$ lie on this diagonal in such a way that $A P=C Q$.
(a) Prove that $\triangle A B P \equiv \triangle C D Q$.
(b) Prove that $\triangle A D P \equiv \triangle C B Q$.
(c) Hence prove that $B Q D P$ is a parallelogram.
(b) $A B C D$ is a parallerogram.

Question 2
In the diagram, $A B C D$ is a quadrilateral in which the diagonals meet at $M$, with $A M=M C$ and $B M=M D$.
(a) Prove $\triangle A B M \equiv \triangle C D M$.
(b) Hence prove that quadrilateral $A B C D$ is a parallelogram.

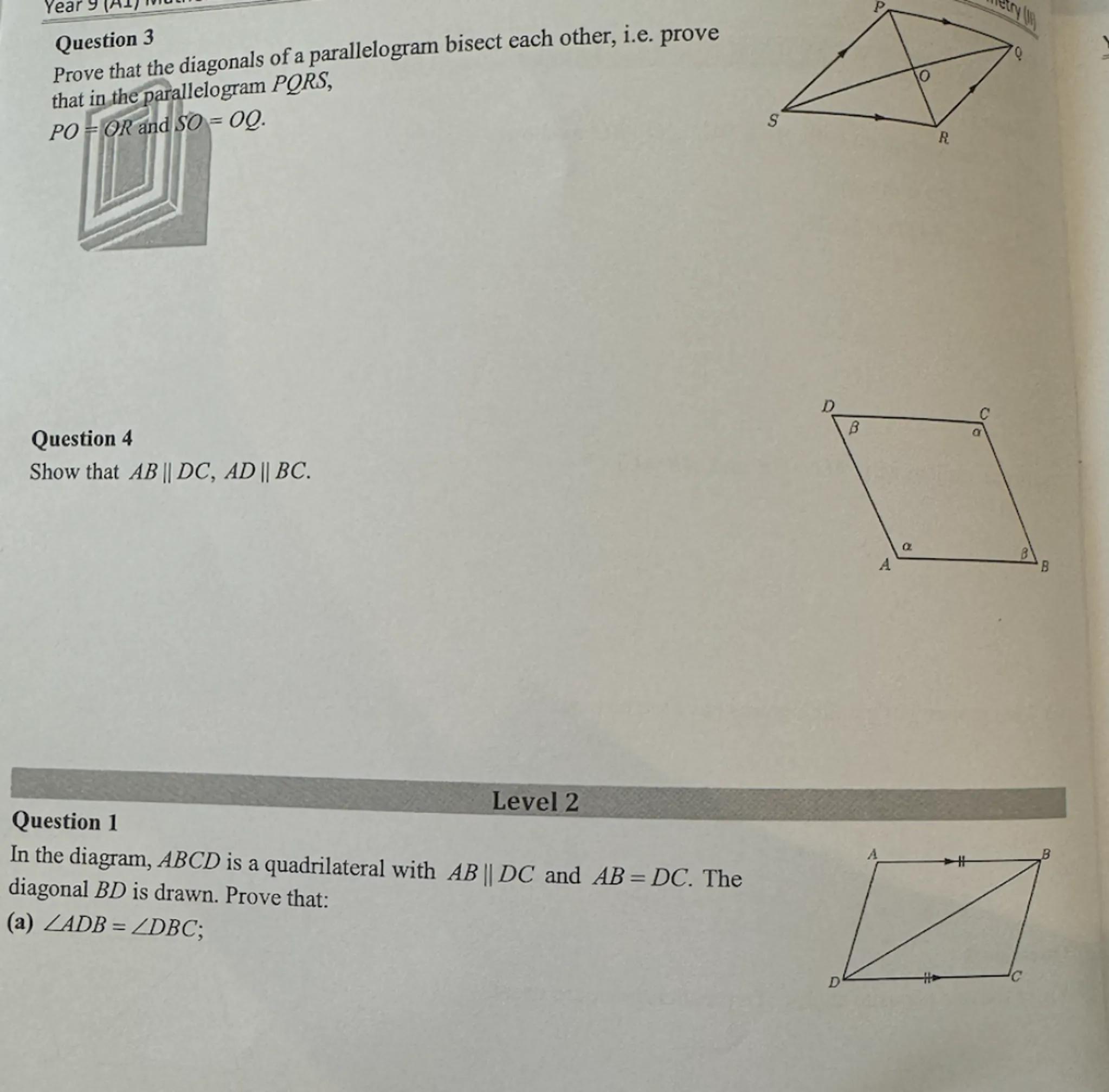
Question 3
$P Q R S$ is a parallelogram, $Q R T$ and $P M T$ are straight lines and $M$ is the midpoint of SR.
(a) Prove that $\triangle P M S \equiv \triangle T M R$.
Question 3
Prove that the diagonals of a parallelogram bisect each other, i.e. prove that in the parallelogram $P Q R S$,

Question 4
Show that $A B\|D C, A D\| B C$.
Level 2

Question 1
In the diagram, $A B C D$ is a quadrilateral with $A B \| D C$ and $A B=D C$. The diagonal $B D$ is drawn. Prove that:
(a) $\angle A D B=\angle D B C$;
Year 9 (A1) Mathematics
(b) Prove that the triangles $A B C$ and $D C B$ are congruent.
Plane Geometry (II)
(c) Deduce that $\angle A B D=\angle D C A$.

Question 4
$A B C D$ is a quadrilateral. The diagonals $A C$ and $B D$ intersect at $P . A D=B C$ and $A C=B D$.
(a) Show that triangles $A B C$ and $A B D$ are congruent.
(b) Show that triangle $A B P$ is isosceles.
c) Hence show that triangle $C D P$ is isosceles.

Show that $A B$ is parallel to $C D$.
Year 9 (A1) Mathematics
(b) Prove that the triangles $A B C$ and $D C B$ are congruent.
Plane Geometry (II)
(c) Deduce that $\angle A B D=\angle D C A$.

Question 4
$A B C D$ is a quadrilateral. The diagonals $A C$ and $B D$ intersect at $P . A D=B C$ and $A C=B D$.
(a) Show that triangles $A B C$ and $A B D$ are congruent.
(b) Show that triangle $A B P$ is isosceles.
c) Hence show that triangle $C D P$ is isosceles.

Show that $A B$ is parallel to $C D$.

0 Like

1 Answer

Share

Add Answer