
Sia

Question
Math
Posted 5 months ago
Chrome
File
Edit
View
History
Bookmarks
Profiles
Tab
Window
Help
A
64\%
Fri Sep 20 16:14
chem 040 - Google Docs
Manage writing suggestions
Submit Homework (Week 3)
Mathway | Calculus Problem
New Tab
gradescope.com/courses/849437/assignments/4968588/submissions/new
Relaunch to update
All Bookmarks
0/3 Questions Answered
View fullscreen
Let nave the ronowing grapn:
(a) Compute the limit .
(b) Compute . How does this compare to the function evaluated at ?
(c) Does the limit exist? Explain why or why not.
B. Please select file(s) 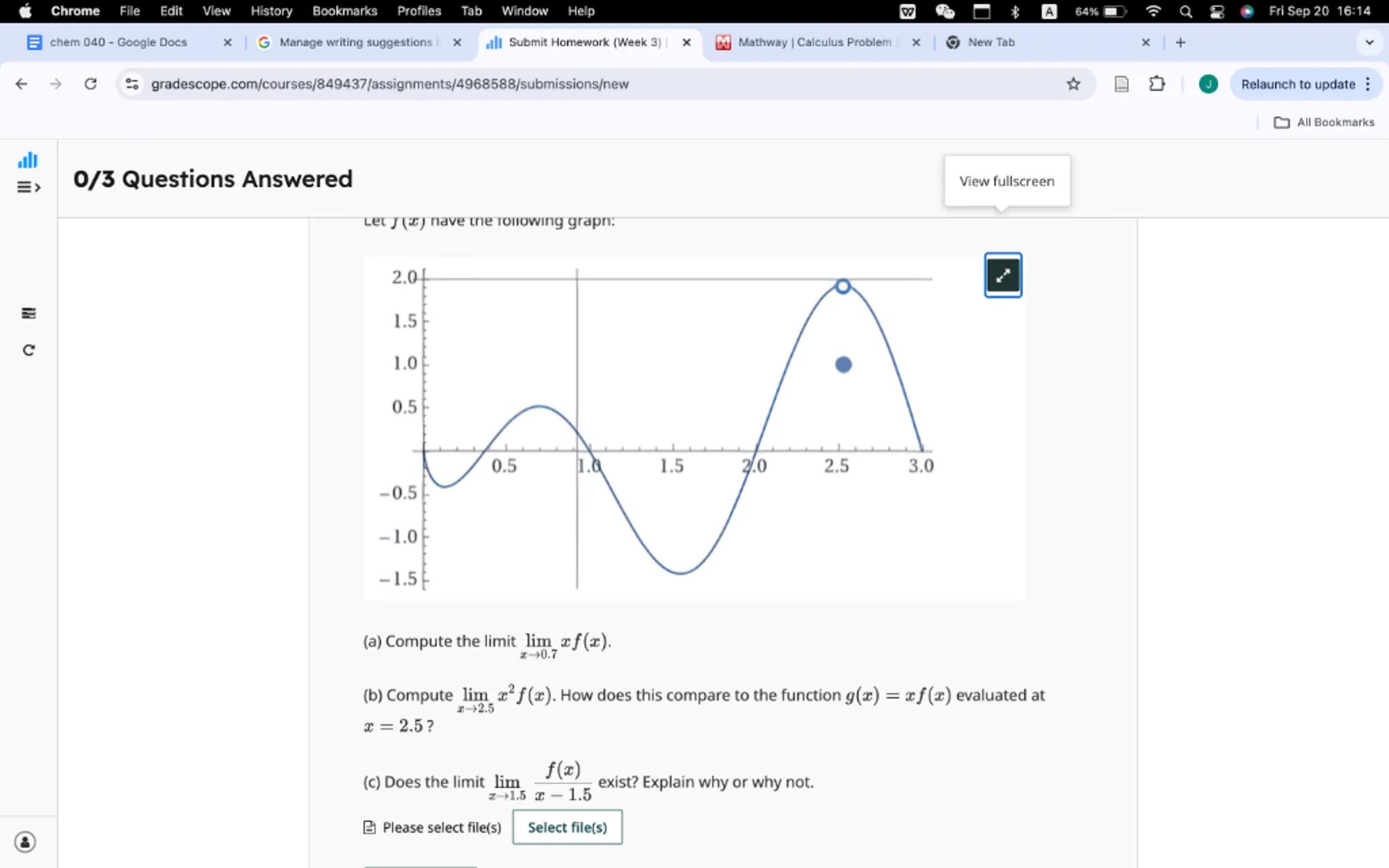

Answer from Sia
Posted 5 months ago
Solution by Steps
step 1
To compute the limit as approaches of , we evaluate . The value of can be determined from the graph
step 2
For the limit , we find from the graph and then compute . This will give us the value of the limit
step 3
To compare this with evaluated at , we calculate and compare the two results
step 4
For the limit , we need to check if approaches as approaches . If , then the limit exists; otherwise, it does not
Answer
The limits and comparisons will depend on the specific values of at the points of interest from the graph.
Key Concept
Understanding limits and their evaluation using graphical information is crucial in calculus.
Explanation
The limits help us understand the behavior of functions at specific points, and comparing different functions at those points provides insight into their relationships.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question