
Sia

Question
Math
Posted 10 months ago
Carbon-14 is an element which loses exactly half of its mass every 5730 years. The mass of a sample of carbon-14 can be modeled by a function, , which depends on its age, (in years).
We measure that the initial mass of a sample of carbon-14 is 741 grams.
Write a function that models the mass of the carbon-14 sample remaining years since the initial measurement.
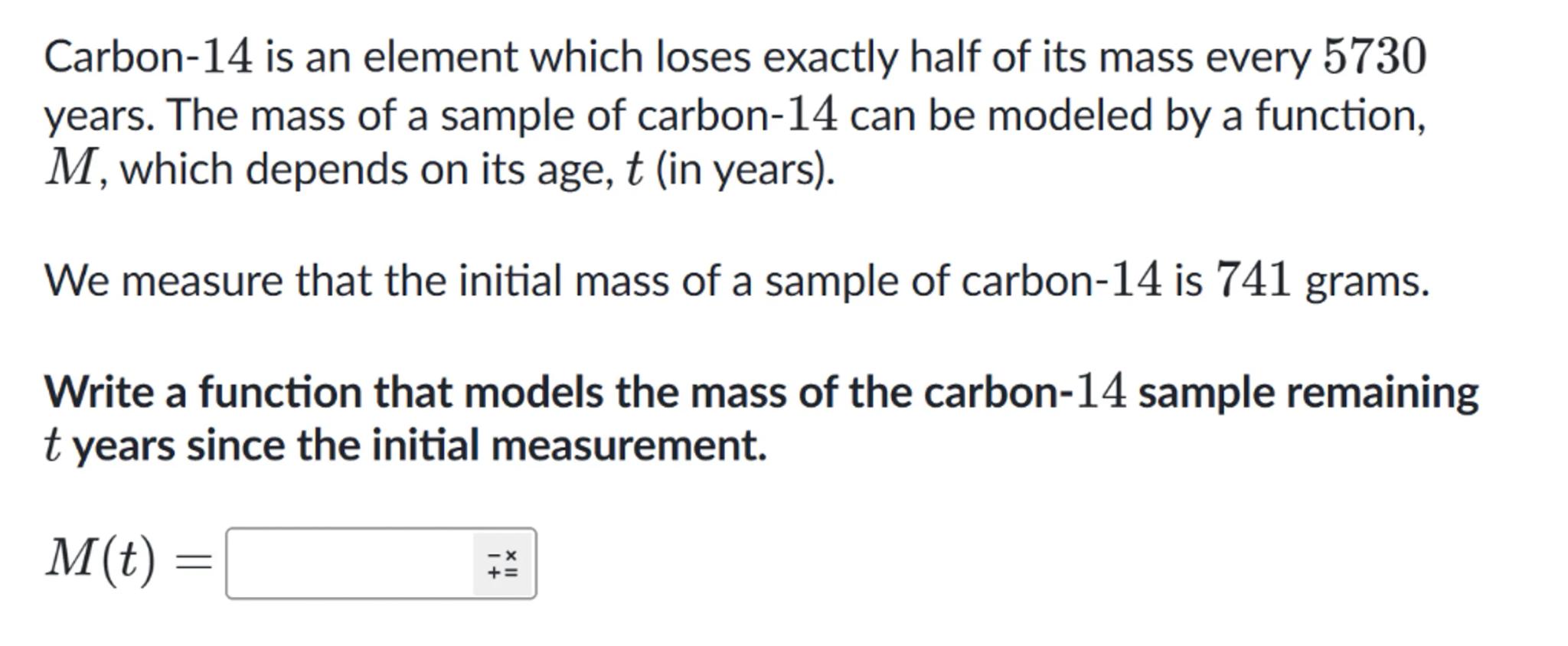

Answer from Sia
Posted 10 months ago
Solution by Steps
step 1
To model the decay of Carbon-14, we use the exponential decay formula, which is , where is the initial mass and is the half-life of the substance
step 2
Given that the initial mass is 741 grams and the half-life is 5730 years, we substitute these values into the formula to get
step 3
Simplifying the expression, we have . This is the function that models the remaining mass of the Carbon-14 sample after years
[1] Answer
Key Concept
Exponential Decay
Explanation
The function represents the exponential decay of Carbon-14, where the mass halves every 5730 years.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question