
Sia

Question
Math
Posted 9 months ago
A sector with a central angle measure of has a radius of .
What is the area of the sector?
Choose 1 answer:
(A)
(B)
(C)
(D) 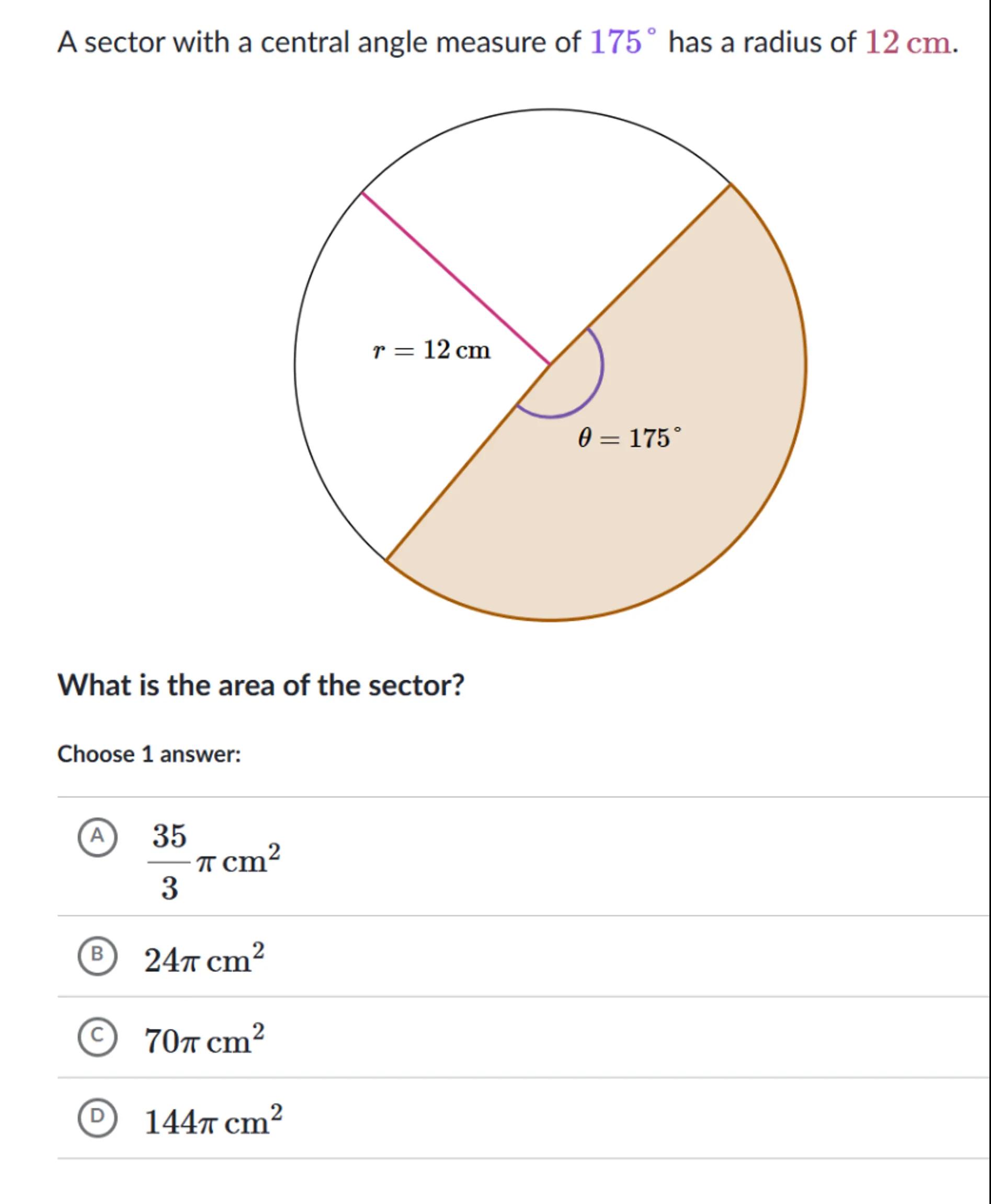

Answer from Sia
Posted 9 months ago
Solution by Steps
step 2
First, we convert the central angle from degrees to radians. Since is equivalent to radians, is radians
step 3
Now we can substitute the values into the formula:
step 4
Simplifying the expression, we get
step 5
The area of the sector is therefore
C
Key Concept
Area of a Sector
Explanation
The area of a sector is calculated by the formula , where the angle must be in radians.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question