
Sia

Question
Math
Posted 10 months ago
A large school district knows that of students in previous years rode the bus to school. Administrators wondered if that figure was still accurate, so they took a random sample of students and found that of those sampled rode the bus to school.
To see how likely a sample like this was to happen by random chance alone, the school district performed a simulation. They simulated 120 samples of students from a large population where of the students rode the bus to school. They recorded the proportion of students who rode the bus in each sample. Here are the sample proportions from their 120 samples:
They want to test vs. where is the true proportion of students in this district that ride the bus to school.
Based on these simulated results, what is the approximate -value of the test?
Note: The sample result was .
Choose 1 answer:
(A) -value
(B) -value
(C) -value
(D) -value 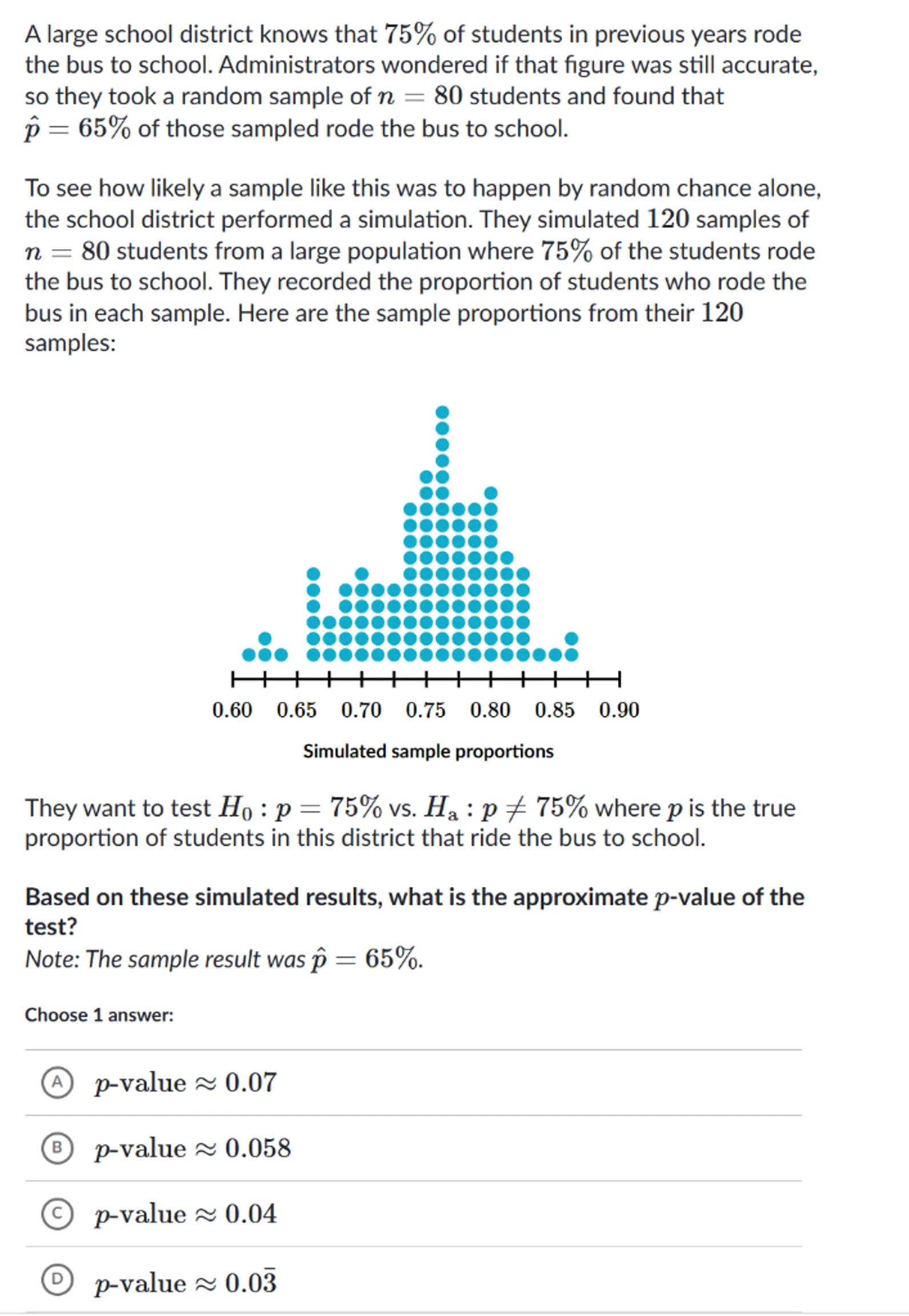

Answer from Sia
Posted 10 months ago
Solution by Steps
step 1
Identify the observed sample proportion and the null hypothesis proportion
step 2
Determine the number of simulated proportions that are as extreme or more extreme than the observed sample proportion
step 3
Calculate the approximate p-value by dividing the number of extreme simulated proportions by the total number of simulations
Answer
The approximate p-value of the test is not provided in the question, but it would be calculated using the steps above.
Key Concept
p-value in hypothesis testing
Explanation
The p-value represents the probability of obtaining a sample proportion as extreme as the observed one (or more extreme) under the assumption that the null hypothesis is true. It is calculated by comparing the observed sample proportion to the distribution of sample proportions from the simulation.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question