
Sia

Question
Math
Posted 10 months ago
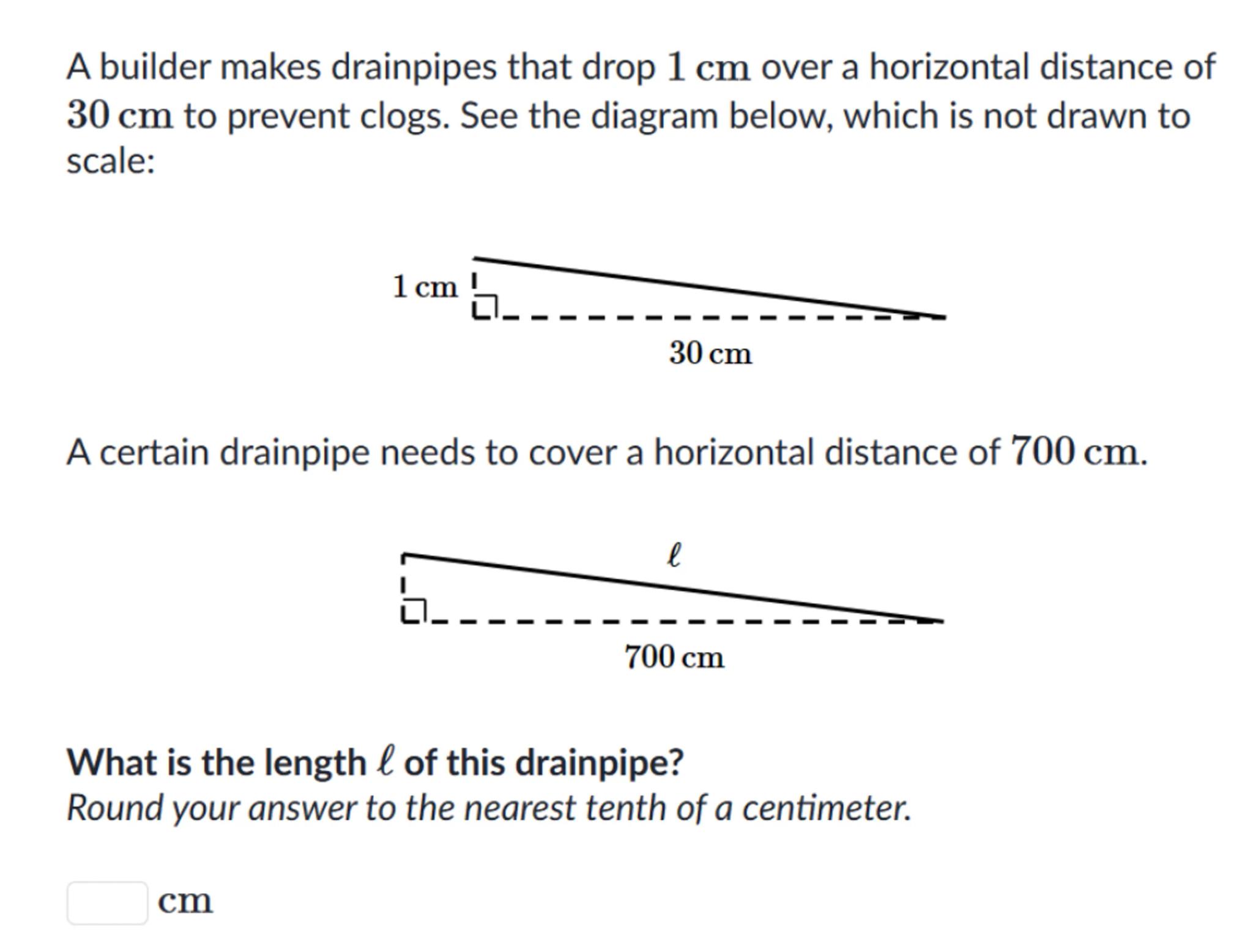
A builder makes drainpipes that drop over a horizontal distance of to prevent clogs. See the diagram below, which is not drawn to scale:
A certain drainpipe needs to cover a horizontal distance of .
What is the length of this drainpipe?
Round your answer to the nearest tenth of a centimeter.

Answer from Sia
Posted 10 months ago
Solution by Steps
step 1
To find the length of the drainpipe, we use the similarity of the two right triangles. The triangles are similar because they both have a right angle and they share the angle where the hypotenuse and the horizontal side meet, making the third angles equal by the Angle-Angle Similarity Postulate
step 2
The ratio of the vertical side to the horizontal side for the smaller triangle is . This ratio will be the same for the larger triangle because of the similarity
step 3
Set up a proportion using the corresponding sides of the similar triangles: , where is the vertical side of the larger triangle
step 4
Solve the proportion for :
step 5
Use the Pythagorean theorem for the larger triangle:
step 6
Substitute into the equation:
step 7
Calculate :
step 8
Simplify and solve for :
step 9
Calculate the value of and round to the nearest tenth:
[1] Answer
cm
Key Concept
Similar Triangles and the Pythagorean Theorem
Explanation
The length of the drainpipe is found by using the properties of similar triangles to determine the length of the missing side and then applying the Pythagorean theorem to find the hypotenuse, which is the length of the drainpipe. The answer is rounded to the nearest tenth as required.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question