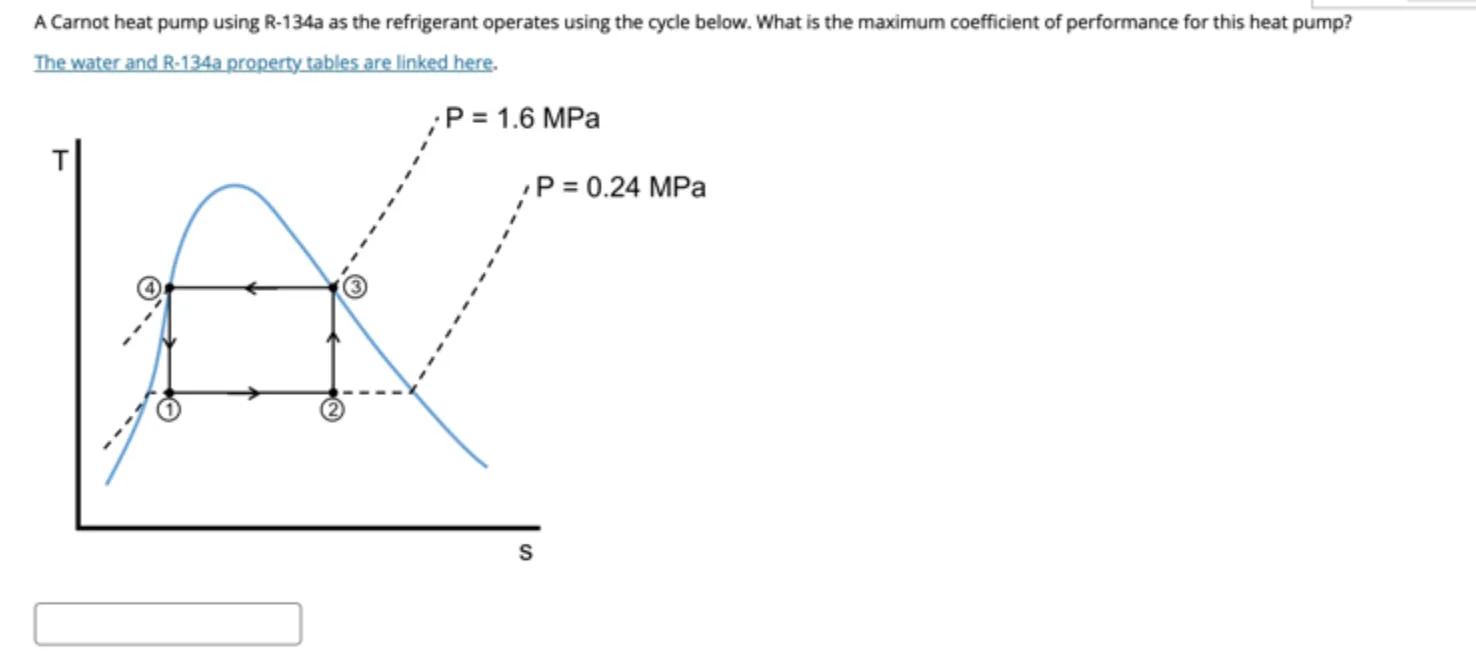
A Carnot heat pump using R-134a as the refrigerant operates using the cycle below. What is the maximum coefficient of performance for this heat pump?
The water and R-134a property tables are linked here.
$\square$

Question

Accepted Answer

∻Solution∻ ‖ a ⋮ To determine the maximum coefficient of performance (COP) for the Carnot heat pump, we use the formula for COP of a heat pump, which is given by: $$COP_{max} = \frac{T_H}{T_H - T_C}$$ where $T_H$ is the temperature of the hot reservoir and $T_C$ is the temperature of the cold reservoir. We need to extract these temperatures from the graph at the respective pressure levels. ‖ ‖ b ⋮ From the graph, identify the temperatures corresponding to the pressures $P = 0.24 \text{ MPa}$ and $P = 1.6 \text{ MPa}$. The temperature at $P = 0.24 \text{ MPa}$ (Point 1) and $P = 1.6 \text{ MPa}$ (Point 3) can be read directly from the y-axis. Let's denote these temperatures as $T_C$ and $T_H$ respectively. ‖ ‖ c ⋮ Substitute the values of $T_H$ and $T_C$ into the COP formula to calculate the maximum COP. Ensure that the temperatures are in Kelvin for the calculation. The final expression will be: $$COP_{max} = \frac{T_H}{T_H - T_C}$$. ‖ ∻Answer∻ ⚹ [Insert final answer here] ⚹ ∻Key Concept∻ ⚹ Carnot Cycle and Coefficient of Performance: The Carnot cycle represents an idealized thermodynamic cycle that provides the maximum efficiency for heat pumps and refrigerators. The COP is a measure of the efficiency of a heat pump, defined as the ratio of heat delivered to the work input. The maximum COP is achieved when the heat pump operates between two thermal reservoirs. ⚹ ∻Explanation∻ ⚹ The maximum COP can be calculated using the temperatures of the hot and cold reservoirs obtained from the graph. This reflects the efficiency of the heat pump in transferring heat from the cold to the hot reservoir. ⚹

Sia