
Sia
100% correct great!
5. The graphs of the functions and are shown in the figure for . It is known that for . The twice-differentiable function , which is not explicitly given, satisfies and .
(a) Find the area of the shaded region enclosed by the graphs of and .
(b) Evaluate the improper integral , or show that the integral diverges.
(c) Let be the function defined by . Find the value of .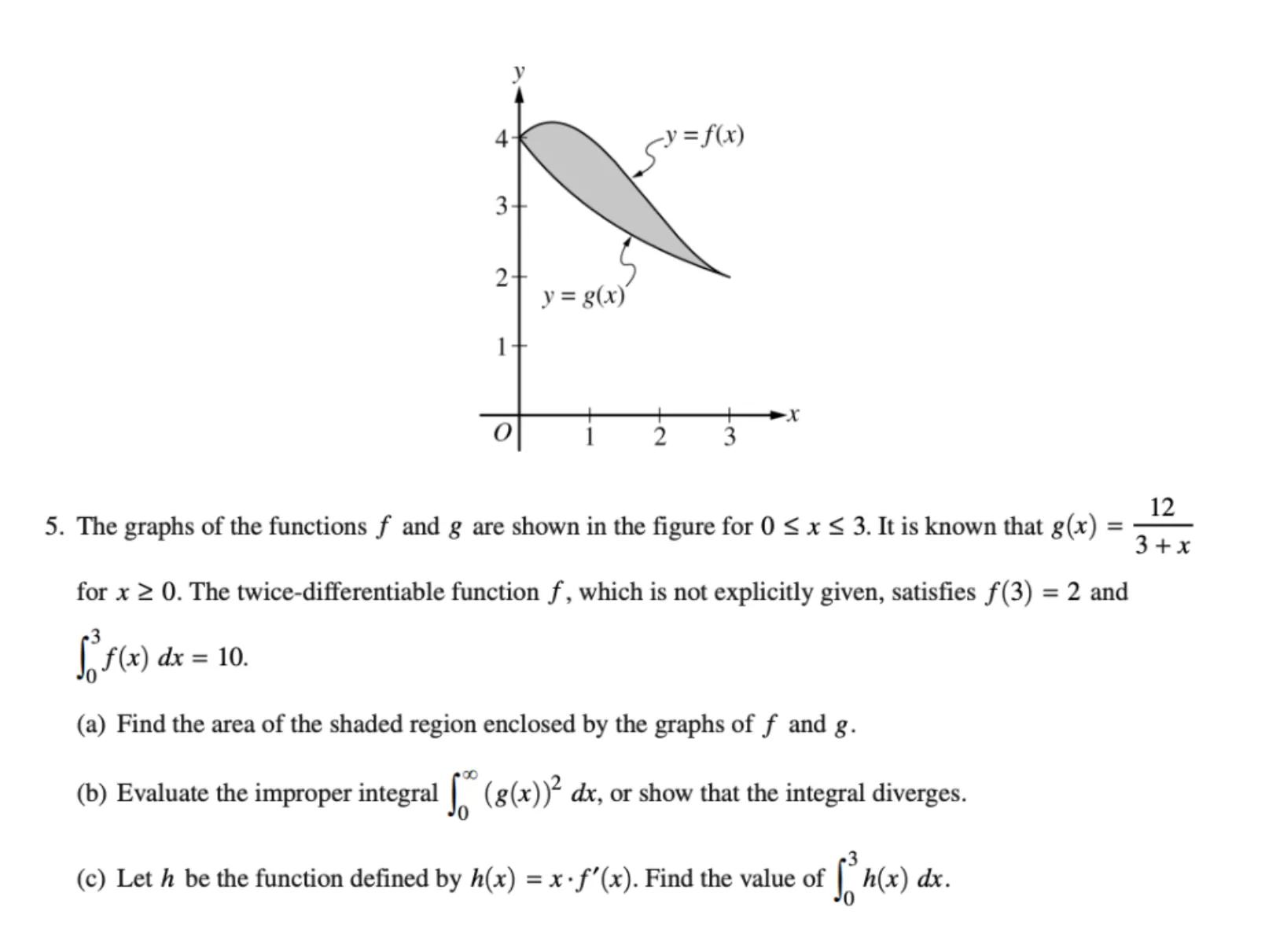

Answer from Sia
Posted 9 months ago
Solution by Steps
step 1
To find the area of the shaded region between the graphs of and from to , we need to compute the integral of the difference between and
step 2
The area is given by the integral:
step 3
We know and
step 4
Compute :
step 5
The area is then:
Part (b)
step 1
To evaluate the improper integral , we first express :
step 2
The integral becomes:
step 3
Use the substitution , hence :
Part (c)
step 1
To find where , we use integration by parts. Let and
step 2
Then and . Using integration by parts:
step 3
Evaluate the boundary term:
step 4
We know , so:
Answer
(a)
(b)
(c)
Key Concept
Area between curves, improper integrals, and integration by parts
Explanation
The area between curves is found by integrating the difference of the functions. Improper integrals require limits to evaluate. Integration by parts is used to integrate products of functions.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
