
Sia
5) Molecular orbitals can have very complicated appearances, but some orbitals shapes can be predicted just from the simple models that you have seen in class, for example orbitals of polyenes and aromatics can be drawn as combinations of orbitals, including phase of the wavefunction, as shown in the orbital here.
a) Use the Particle in a Box model and p orbital shape to sketch the four unique orbitals of butadiene . Rank them from lowest to highest energy.
b) The Particle on a Ring and the orbital shape can be used to create the six unique orbitals of benzene. (i) Draw two of these orbitals that form a degenerate pair and (ii) explain why their shapes show that they must have the same energy; include phase. Extra copies are given if you want to start over; indicate which pair is to be marked.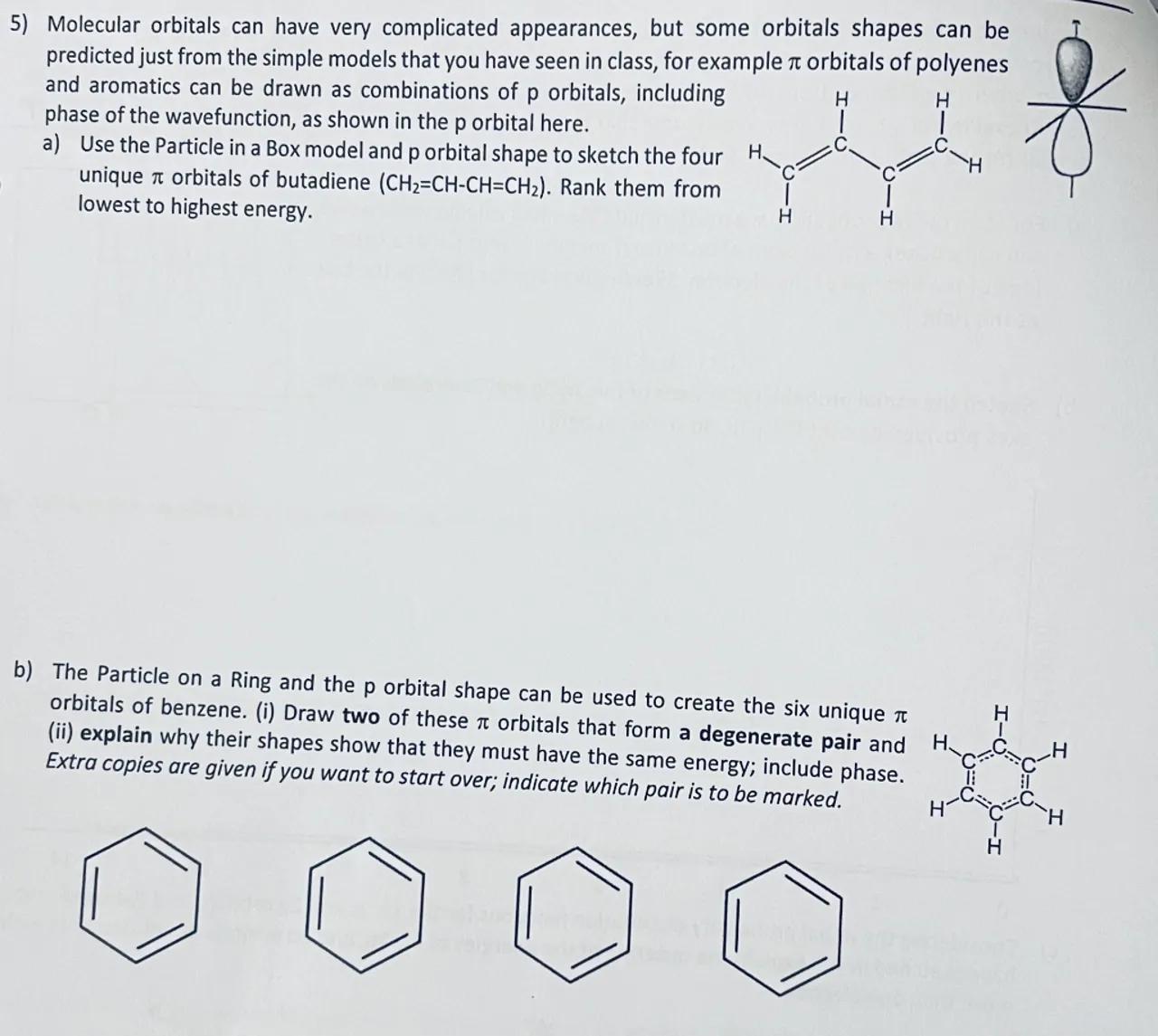

Answer from Sia
Posted 10 months ago
Solution
1
Sketch the pi orbitals of butadiene: To sketch the four unique pi orbitals of butadiene using the Particle in a Box model, we consider the molecule as a box with a length proportional to the number of carbon atoms involved in the conjugation. The p orbitals on each carbon atom combine to form pi molecular orbitals
2
Rank the pi orbitals: The energy of the pi orbitals increases with the number of nodes. The lowest energy orbital (π1) has no nodes, the next (π2) has one node, and so on. The order from lowest to highest energy is π1 < π2 < π3 < π4
3
Draw the degenerate pi orbitals of benzene: Using the Particle on a Ring model for benzene, the six p orbitals combine to form six pi molecular orbitals. Two of these orbitals will have the same energy and are thus degenerate
4
Explain the degeneracy: The degenerate orbitals have the same number of nodes and the same symmetry, which results in the same energy. The phase of the wavefunction (indicated by the shading or sign of the wavefunction) is also the same for both orbitals in the degenerate pair
1 Answer
The four unique pi orbitals of butadiene are sketched based on the Particle in a Box model, with the energy increasing from π1 to π4. The degenerate pi orbitals of benzene are drawn using the Particle on a Ring model, and their degeneracy is explained by their identical number of nodes, symmetry, and phase.
Key Concept
Molecular orbital theory and particle models
Explanation
The Particle in a Box and Particle on a Ring models are used to predict the shapes and energy levels of pi molecular orbitals in conjugated systems like butadiene and benzene.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question