
Sia
4 (a) By considering , use the method of differences to prove that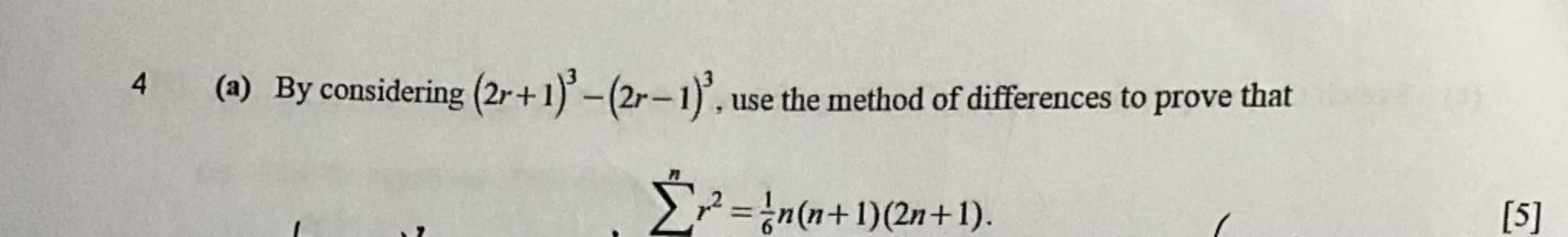

Answer from Sia
Posted 5 months ago
Solution by Steps
step 1
We start with the expression . By expanding both cubes, we can simplify this expression
step 2
The expansion gives us
step 3
Now, we can express the sum of from to using the formula:
step 4
This formula can be derived using the method of differences, which involves finding the difference between consecutive terms and summing them up
Answer
The sum of from to is .
Key Concept
The method of differences is a technique used to derive summation formulas by analyzing the differences between terms.
Explanation
The answer shows that the sum of squares can be expressed in a closed form, which is useful for calculating sums efficiently.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
