Asksia AI LOGO

Sia

704656448's Question
Statistics
Posted 4 months ago

22:06 10月20日周日
16%16 \%
HW4
HW4
开始
插入
页面
审阅
衩图
效室
R. WPS AI
Times.
小四
A∗\mathrm{A}^{*}
A−\mathrm{A}^{-}
B
II
U‾\underline{U}
A
A′A^{\prime}
A
正文
播入
大纲
设置的标影会在此处显示
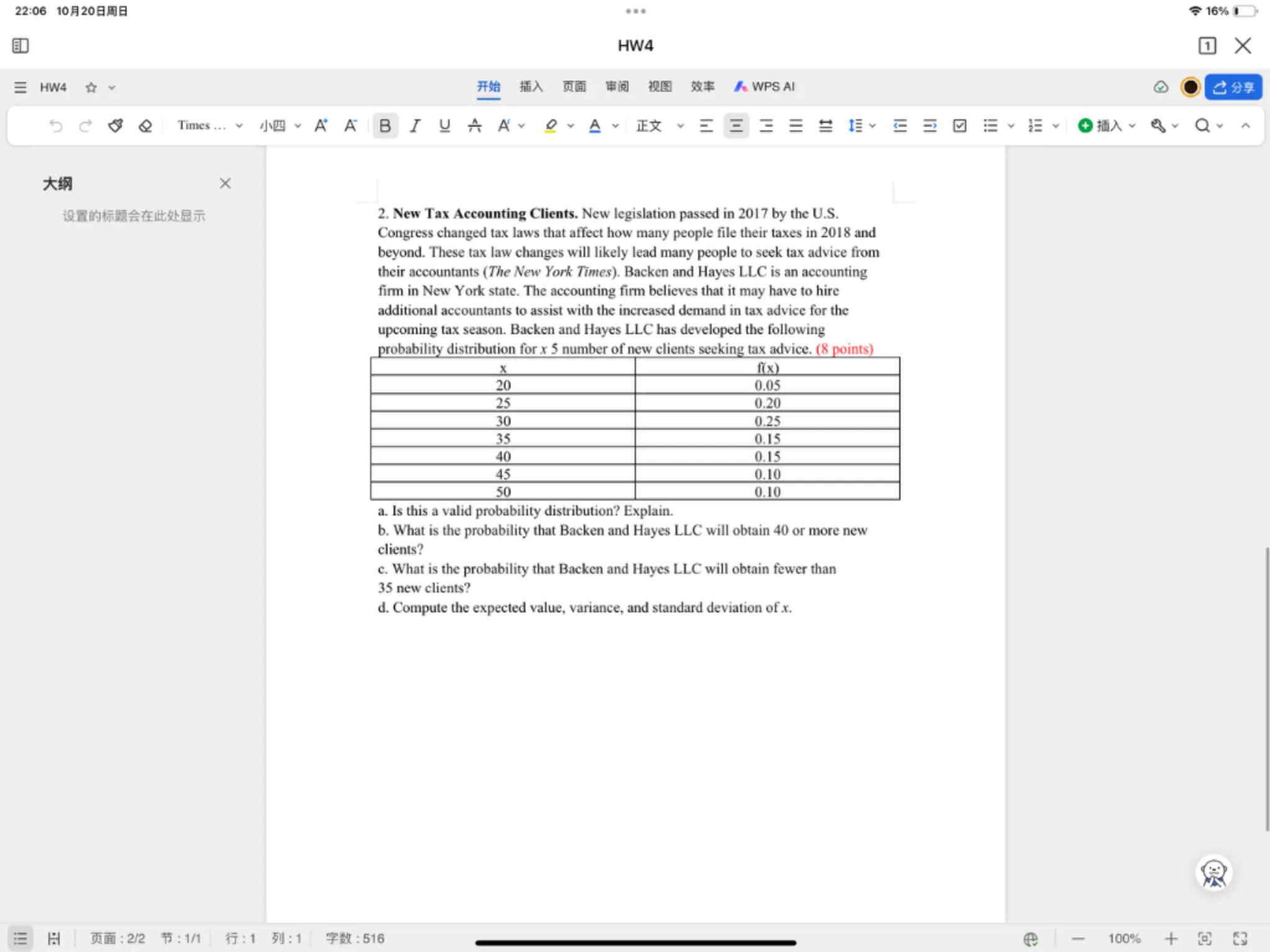
2. New Tax Accounting Clients. New legislation passed in 2017 by the U.S. Congress changed tax laws that affect how many people file their taxes in 2018 and beyond. These tax law changes will likely lead many people to seek tax advice from their accountants (The New York Times). Backen and Hayes LLC is an accounting firm in New York state. The accounting firm believes that it may have to hire additional accountants to assist with the increased demand in tax advice for the upcoming tax season. Backen and Hayes LLC has developed the following probability distribution for x5x 5 number of new clients seeking tax advice. ( 8 points)
\begin{tabular}{|c|c|}
\hlinexx & f(x)f(x) \\
\hline 20 & 0.05 \\
\hline 25 & 0.20 \\
\hline 30 & 0.25 \\
\hline 35 & 0.15 \\
\hline 40 & 0.15 \\
\hline 45 & 0.10 \\
\hline 50 & 0.10 \\
\hline
\end{tabular}
a. Is this a valid probability distribution? Explain.
b. What is the probability that Backen and Hayes LLC will obtain 40 or more new clients?
c. What is the probability that Backen and Hayes LLC will obtain fewer than

35 new clients?
d. Compute the expected value, variance, and standard deviation of xx.
页面：2/2 节：1/1
行:1 列:1
字数: 516
100%100 \%
Sign in to unlock the answer
Answer from Sia
Posted 4 months ago
Solution by Steps
step 1
To determine if the probability distribution is valid, we need to check if the sum of all probabilities equals 1: ∑f(x)=0.05+0.20+0.25+0.15+0.15+0.10+0.10=1.00 \sum f(x) = 0.05 + 0.20 + 0.25 + 0.15 + 0.15 + 0.10 + 0.10 = 1.00
step 2
The probability that Backen and Hayes LLC will obtain 40 or more new clients is calculated by summing the probabilities for x=40,45, x = 40, 45, and 50 50 : P(x≥40)=f(40)+f(45)+f(50)=0.15+0.10+0.10=0.35 P(x \geq 40) = f(40) + f(45) + f(50) = 0.15 + 0.10 + 0.10 = 0.35
step 3
The probability that Backen and Hayes LLC will obtain fewer than 35 new clients is calculated by summing the probabilities for x=20,25,30 x = 20, 25, 30 : P(x<35)=f(20)+f(25)+f(30)=0.05+0.20+0.25=0.50 P(x < 35) = f(20) + f(25) + f(30) = 0.05 + 0.20 + 0.25 = 0.50
step 4
To compute the expected value E(x) E(x) , we use the formula: E(x)=∑(x⋅f(x))=20⋅0.05+25⋅0.20+30⋅0.25+35⋅0.15+40⋅0.15+45⋅0.10+50⋅0.10=33.25 E(x) = \sum (x \cdot f(x)) = 20 \cdot 0.05 + 25 \cdot 0.20 + 30 \cdot 0.25 + 35 \cdot 0.15 + 40 \cdot 0.15 + 45 \cdot 0.10 + 50 \cdot 0.10 = 33.25
step 5
The variance Var(x) Var(x) is calculated using the formula: Var(x)=E(x2)−(E(x))2 Var(x) = E(x^2) - (E(x))^2 where E(x2)=∑(x2⋅f(x)) E(x^2) = \sum (x^2 \cdot f(x)) . First, we compute E(x2) E(x^2) : E(x2)=202⋅0.05+252⋅0.20+302⋅0.25+352⋅0.15+402⋅0.15+452⋅0.10+502⋅0.10=1135.00 E(x^2) = 20^2 \cdot 0.05 + 25^2 \cdot 0.20 + 30^2 \cdot 0.25 + 35^2 \cdot 0.15 + 40^2 \cdot 0.15 + 45^2 \cdot 0.10 + 50^2 \cdot 0.10 = 1135.00 Then, Var(x)=1135.00−(33.25)2=1135.00−1105.5625=29.4375 Var(x) = 1135.00 - (33.25)^2 = 1135.00 - 1105.5625 = 29.4375
step 6
The standard deviation SD(x) SD(x) is the square root of the variance: SD(x)=Var(x)=29.4375≈5.43 SD(x) = \sqrt{Var(x)} = \sqrt{29.4375} \approx 5.43
Answer
A
Key Concept
Probability distribution validity, expected value, variance, and standard deviation
Explanation
A valid probability distribution sums to 1, and we can compute probabilities, expected value, variance, and standard deviation from the given distribution.

Not the question you are looking for? Ask here!

Enter question by text

Enter question by image

Unlock Smarter Learning with AskSia Super!

Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.

30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question